Raconte-moi... le SLE
par Vincent Beffara
Introduction
Soit $n$ un entier positif: une marche auto-évitante de longueur $n$ sur le réseau $\mathbb Z^2$ est un chemin discret $(x_i)_{0 \leqslant i \leqslant n}$ issu de $x_0=0$, tel que $x_i$ et $x_{i+1}$ soient voisins pour tout $i$, et tel que les $x_i$ soient tous distincts. L'ensemble $\Omega_n$ des marches auto-évitantes de longueur $n$ est fini, et il est facile de montrer par un argument de sous-multiplicativité que son cardinal $c_n$ satisfait à $$\frac1n \log c_n \xrightarrow[n\to\infty]{} \log \mu$$ avec $\mu\in(2,3)$, appelé constante de connectivité de $\mathbb Z^2$. C'est à peu près tout ce qu'on sait des marches auto-évitantes en dimension $2$! En particulier on ne connaît pas la valeur exacte de $\mu$.
Les conjectures ne manquent pas. La plus facile à énoncer concerne toujours $c_n$: les physiciens prédisent que $$c_n = \mu^n n^{11/32+o(1)}.$$ Le comportement d'une longue marche auto-évitante ''typique'' (tirée au sort uniformément dans $\Omega_n$ avec $n$ grand) reste également mystérieux: on conjecture que l'extrémité fluctue plus que celle d'une marche aléatoire simple, et que $$E[\|x_n\|^2] = n^{4/3 + o(1)}$$ (pour la marche simple, le théorème central limite donne un exposant $1$ au lieu de $4/3$). Ces valeurs $4/3$, $11/32$,... portent le nom d'exposants critiques, et on pense qu'ils sont universels: sur un autre réseau de dimension $2$, $\mu$ sera différent mais les exposants seraient les mêmes.
Plus généralement, on s'attend à ce qu'une telle grande marche ait une limite d'échelle, c'est-à-dire que renormalisée par son diamètre, elle converge en loi (dans la limite $n\to\infty$) vers une certaine courbe aléatoire dans le plan, comme la marche simple converge vers le mouvement brownien.
La question de la convergence reste entièrement ouverte, mais on sait quelle est cette courbe limite si elle existe: il s'agit d'une variante du processus appelé ''SLE'', un objet introduit par Oded Schramm en 2000 et dont l'étude a fondamentalement changé la compréhension que les mathématiciens ont de la mécanique statistique. Les travaux correspondants ont depuis été récompensés par deux médailles Fields (W. Werner en 2006 et S. Smirnov en 2010).

1- Invariance conforme
Le cas de la marche aléatoire simple sur $\mathbb Z^2$ est instructif: sa limite d'échelle est explicite, il s'agit du mouvement brownien plan, qui a l'avantage de se prêter facilement à des calculs. Il a la propriété remarquable suivante: si $U_1$ et $U_2$ sont deux domaines simplement connexes du plan (vu comme le plan complexe) contenant $0$, et si $\Phi : U_1 \overset{\sim}{\rightarrow} U_2$ est une bijection conforme envoyant $0$ sur lui-même, alors pour un mouvement brownien $(B_t)$ arrêté à sa sortie de $U_1$, le processus $(\Phi(B_t))$ est lui-même un mouvement brownien, arrêté à sa sortie de $U_2$ (à un changement de temps près).
Ce phénomène, observé pour la première fois par Lévy (1965), porte le nom d'invariance conforme, et les physiciens prédisent qu'il devrait apparaître dans de nombreux modèles de mécanique statistique. Ils l'expliquent par la méthode du groupe de renormalisation, qui permet de comprendre (de manière le plus souvent non rigoureuse) l'apparition de telles symétries supplémentaires à la limite d'échelle, mais les mathématiciens sont loin de pouvoir en faire une étude (mathématiquement) rigoureuse.
Pour formaliser cette intuition dans le cadre qui va nous intéresser, la topologie la plus agréable est la suivante: pour chaque domaine simplement connexe $U$ du plan complexe, muni de deux points marqués $a,b \in \partial U$, on cherche à définir une mesure de probabilité $\mu_{U,a,b}$ sur l'ensemble des courbes simples dans $\overline U$ partant de $a$ et arrivant à $b$ sans toucher $\partial U$ entre-temps. Il est alors naturel d'introduire la définition suivante : une collection $(\mu_{U,a,b})$ de mesures de probabilité a la propriété d'invariance conforme si pour toute bijection conforme $\Phi : U_1 \overset{\sim}{\rightarrow} U_2$ on a l'identité $\mu_{U_2, \Phi(a), \Phi(b)} = \Phi_\ast \mu_{U_1,a,b}$ (autrement dit, si $\gamma$ est une courbe dans $U_1$ de loi $\mu_{U_1, a, b}$ alors son image $\Phi(\gamma)$ a pour loi $\mu_{U_2, \Phi(a), \Phi(b)}$).
Une remarque s'impose, qui nous servira par la suite: le cas où $U_1=U_2$ avec les mêmes points marqués est déjà non trivial, parce que $\Phi$ n'est pas pour autant l'identité, il y a une famille à un paramètre d'applications conformes qui conviennent et $\mu_{U_1,a,b}$ doit être invariante par tous les éléments de cette famille. Si par exemple $U_1$ est la bande $\mathbb B = \mathbb R \times (0,1)$ avec les deux points marqués à l'infini des deux côtés, on voit que $\mu_{\mathbb B, -\infty, +\infty}$ doit être invariante par translation le long de $\mathbb B$. Dans le demi-plan supérieur $\mathbb H$ avec comme points marqués $0$ et $\infty$, $\mu_{\mathbb H,0,\infty}$ doit de même être invariante par changement d'échelle $z \mapsto \lambda z$ pour tout $\lambda>0$.
2- Propriété de Markov de domaine
Une propriété qui est évidente pour la marche auto-évitante uniforme est la suivante: la loi conditionnelle des $n-k$ derniers pas, conditionnellement aux $k$ premiers, est uniforme parmi les continuations possibles de ces $k$ pas. Le même phénomène se produit par exemple dans le cas d'interfaces pour des modèles de mécanique statistique n'ayant que des interactions entre plus proches voisins (comme typiquement le modèle d'Ising).
Dans le cas qui nous intéresse, on voudrait formaliser l'intuition suivante: dans un domaine $U$, le futur de $\gamma$ sachant que son segment initial suit une portion de courbe $\delta$ a la même loi qu'une courbe dans le domaine $U \setminus \delta$, et partant de l'extrémité de $\delta$. En notant $\delta^\ast$ cette extrémité et $\mu^\delta_{U,a,b}$ la mesure conditionnée, on dira donc que la collection $(\mu_{U,a,b})$ a la propriété de Markov de domaine si pour tous $U,a,b,\delta$ comme ci-dessus on a $\mu_{U,a,b}^\delta = \mu_{U\setminus\delta, \delta_\ast, b}.$
3- Chaînes de Loewner
L'observation fondamentale de Schramm (2000) est alors la suivante: il n'existe qu'une famille à un paramètre de collections $(\mu_{U,a,b})$ satisfaisant à la fois à l'invariance conforme et à la propriété de Markov de domaine, et on peut les décrire explicitement.
Une façon de le voir est tout d'abord de se ramener (par invariance conforme) au cas où $(U,a,b)$ est le demi-plan supérieur $\mathbb H$ avec comme points marqués $0$ et $\infty$, puis de remarquer que la loi $\mu_{\mathbb H, 0, \infty}$ est alors entièrement déterminée par le comportement au voisinage de $0$ de la courbe. En effet il suffit de réaliser un segment initial $\delta$ selon cette loi, et la loi de la suite de la courbe est alors obtenue comme image de $\mu_{\mathbb H, 0, \infty}$ par une application conforme de $\mathbb H$ vers $\mathbb H \setminus \delta$, qui existe par le théorème de Riemann (autrement dit, on peut ''couper $\gamma$ en tranches'' et sa loi est caractérisée par celle de la première tranche).
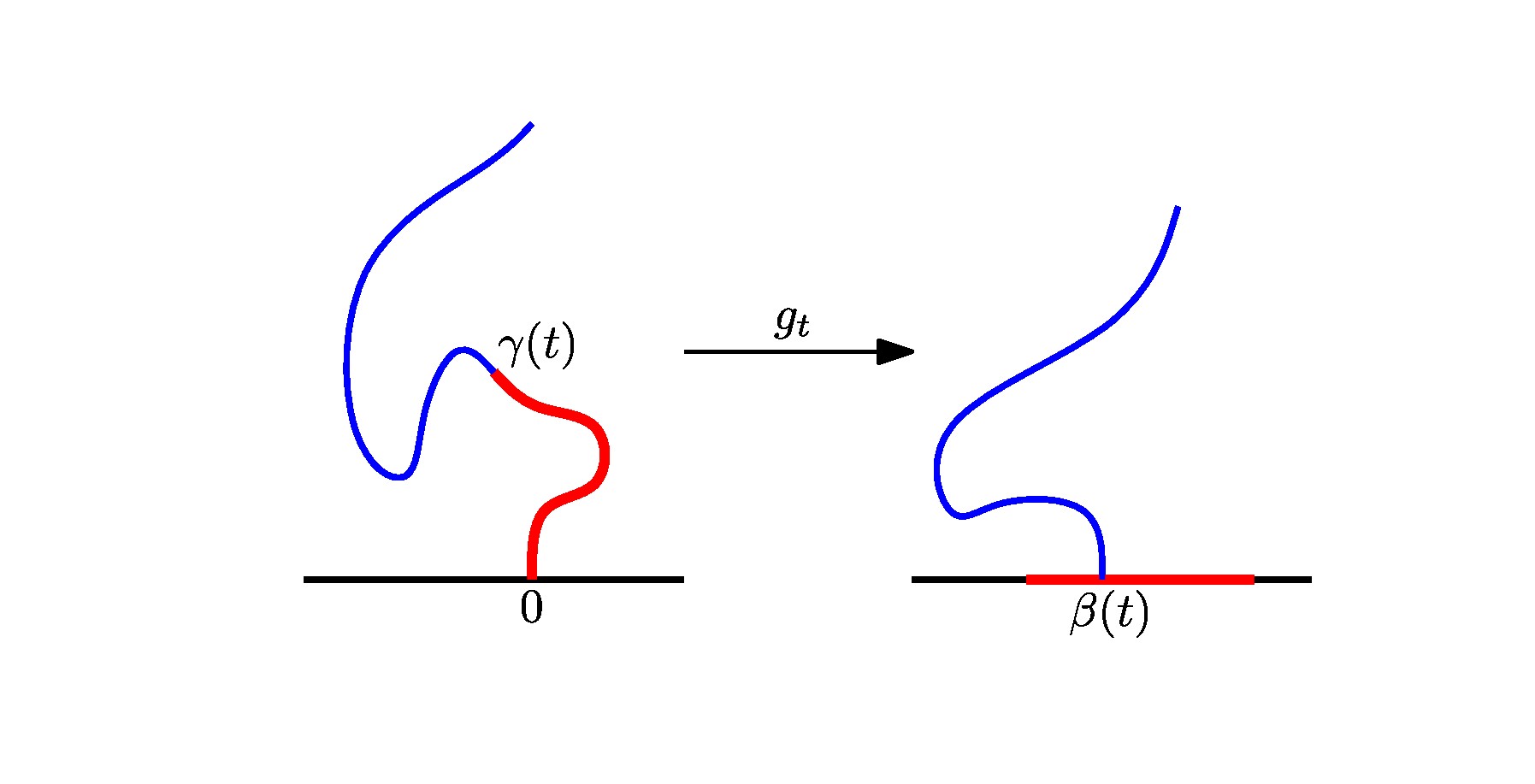
On peut aller plus loin en suivant une stratégie introduite par Loewner (1923) dans un contexte entièrement différent (il cherchait à prouver la conjecture de Bieberbach). Soit donc $\gamma$ une courbe simple dans $\mathbb H$, partant de $0$; pour tout $t \geqslant 0$, notons $H_t = \mathbb H \setminus \gamma([0,t])$ le domaine laissé libre par $\gamma$ au temps $t$, et soit $g_t : H_t \overset{\sim}{\rightarrow} \mathbb H$ l'unique application conforme telle que $g_t(z) = z + \mathcal O(1/z)$ à l'infini. Quitte à effectuer sur $\gamma$ un changement de temps croissant, on peut même supposer que pour tout $t \geqslant 0$, le développement asymptotique de $g_t$ est $$g_t(z) = z + \frac {2t} {z} + \mathcal O(1/z^2).$$
Le théorème de Loewner énonce alors qu'il existe une fonction continue $\beta : \mathbb R_+ \to \mathbb R$ telle que $(g_t)$ soit le flot de l'équation différentielle $$\partial_t g_t(z) = \frac 2 {g_t(z) - \beta(t)}$$ dite équation de Loewner. La fonction $\beta$ peut être identifiée à partir de la courbe en remarquant que $$\beta(t) = g_t(\gamma(t)).$$
4- Le processus SLE
En combinant la construction de Loewner et l'observation de Schramm, l'identification de $(\mu_{U,a,b})$ revient à celle de $\mu_{\mathbb H, 0, \infty}$, et enfin à celle de la fonction $\beta$ correspondante (qui est elle-même aléatoire). L'invariance conforme et la propriété de Markov de domaine se transposent en des propriétés de $\beta$: elle doit avoir des accroissements indépendants et stationnaires (ce qui signifie que la loi de $\beta(t+s)-\beta(t)$ ne dépend pas de $t$), et l'invariance de $\mu_{\mathbb H,0,\infty}$ par changement d'échelle implique qu'en distribution, $$\beta(\lambda t) \stackrel{(d)}= \lambda^2 \beta(t)$$ pour tous $\lambda>0$ et $t \geqslant 0$.
Il est bien connu qu'un processus stochastique satisfaisant à ces conditions doit être un mouvement brownien, à renormalisation près: il existe un paramètre $\kappa \geqslant 0$ tel que $$(\beta(t))_{t \geqslant 0} \stackrel{(d)}= (\sqrt\kappa W_{t}) _{t \geqslant 0}$$ où $W$ désigne un mouvement brownien réel standard. On arrive donc à la définition:
On appelle processus (ou évolution) de Schramm-Loewner de paramètre $\kappa$, ou SLE($\kappa$), la solution de l'équation de Loewner où l'on a posé $\beta(t) = \sqrt\kappa W_{t}$.
Une fois la définition posée, SLE($\kappa$) désigne à la fois la famille $(g_t)$ d'applications conformes obtenues en résolvant l'équation de Loewner, celle $(H_t)$ de leurs domaines de définition, et la courbe $\gamma$ elle-même (qui existe, mais dont l'existence ne va pas de soi à partir de la définition, la preuve de Rohde et Schramm (2005) est extrêmement technique). On peut bien sûr étendre la définition à tout domaine simplement connexe par invariance conforme.
5- Propriétés du SLE
La géométrie de la courbe $\gamma$ dépend fortement de la valeur du paramètre $\kappa$, ce qui est une bonne chose, car différents modèles discrets convergent vers des SLE et il serait surprenant qu'ils aient la même limite d'échelle. Par exemple, il n'est pas difficile de prouver, une fois que l'on sait que la courbe $\gamma$ existe, que (avec probabilité $1$ pour ces énoncés et les suivants):
- si $\kappa\in(0,4]$, $\gamma$ est une courbe simple;
- si $\kappa\in(4,8)$, $\gamma$ n'est pas une courbe simple, mais elle ne se traverse pas (elle «~rebondit sur son passé~»);
- si $\kappa\in[8,+\infty)$, $\gamma$ est surjective de $\mathbb R_+$ vers $\overline{\mathbb H}$ (c'est une courbe de Peano aléatoire).
Par ailleurs, on sait (Beffara 2008) que sa dimension fractale est égale à $1+\kappa/8$ pour tout $\kappa\leqslant8$.



Il est également possible de calculer explicitement la probabilité de différents événements (comme par exemple celle de toucher un intervalle prescrit de la droite réelle, ou celle de passer à droite d'un point de~$\mathbb H$); le fait que tout le processus soit décrit à partir d'un mouvement brownien réel donne accès à tout l'arsenal du calcul stochastique.
Cela donne une stratégie possible pour finir l'identification de la limite d'échelle d'un processus discret: si l'on sait obtenir l'invariance conforme et la propriété de Markov de domaine (qui est en général facile à prouver), tout ce qui reste à déterminer est la valeur du paramètre $\kappa$ et cela peut être fait si l'on sait calculer, pour le modèle discret en question, la limite de la probabilité d'événements du même genre. Hélas, l'invariance conforme n'est pour l'instant connue que dans très peu de cas...
En contrepartie, tout ce que l'on sait prouver sur le SLE se transcrit en retour sur le processus discret et permet souvent d'obtenir des résultats dont l'énoncé est entièrement élémentaire, mais qui sans une telle technologie resteraient inaccessibles.
6- Exemplesd'applications
Le premier cas où l'on a montré la convergence d'un modèle discret vers un SLE est celui de la marche aléatoire à boucles effacées, qui est (comme son nom l'indique) définie à partir de la marche aléatoire simple en supprimant de sa trajectoire toutes les boucles qu'elle forme, de manière chronologique, et ceci jusqu'à ce que la marche sorte d'un domaine discret. Il s'agit d'une marche auto-évitante aléatoire, mais dont la loi n'est pas uniforme, ce n'est donc pas l'objet dont nous sommes partis au début de cette note; mais comme la marche aléatoire converge vers le brownien et que la procédure suivie est purement topologique, il est naturel de s'attendre à ce que la marche à boucles effacées ait pour limite d'échelle le «mouvement brownien à boucles effacées».
La situation n'est pas si simple (parce que le mouvement brownien fait beaucoup trop de boucles à toutes les échelles), mais il reste que l'invariance conforme est vérifiée (Lawler, Schramm et Werner (2004)) et que dans ce cas on sait prouver la convergence vers SLE pour le paramètre $\kappa=2$. Pour revenir au modèle discret, cela permet de comprendre pourquoi après $n$ pas, une marche à boucles effacées se trouve à une distance de l'ordre de $n^{4/5}$ de son point de départ.
D'autres modèles de mécanique statistique, par exemple la percolation (Smirnov (2001)), le modèle d'Ising (Smirnov (2010)) et les arbres couvrants uniformes (Lawler, Schramm et Werner (2004)), ont aussi des SLE pour limites d'échelle, avec à chaque fois une valeur de $\kappa$ différente.
Le mouvement brownien plan lui-même est très lié au processus SLE($6$); en particulier, ils ont des frontières extérieures de lois localement absolument continues l'une par rapport à l'autre. L'étude du SLE permet alors de prouver une conjecture due à Mandelbrot: la frontière extérieure du mouvement brownien a pour dimension $4/3$ (cf. Lawler, Schramm et Werner (2001a)).
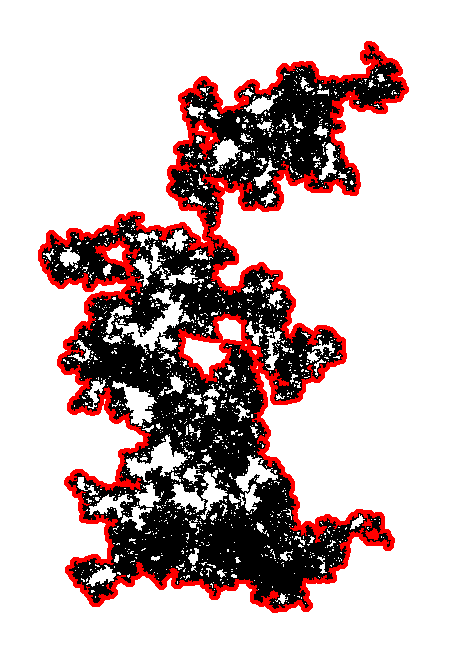
Un dernier exemple, dont l'énoncé est entièrement élémentaire: soient $(X_n)$ et $(Y_n)$ deux marches aléatoires simples sur $\mathbb Z^2$, issues de $0$, et soit, pour $N>0$, $p_N$ la probabilité que les trajectoires \mbox{$\{X_n : 1<n\leqslant N\}$} et $\{Y_n : 1<n\leqslant N\}$ soient disjointes. Alors par Lawler, Schramm et Werner (2001b, 2001c), $$p_N = N^{- \frac 5 8 + o(1)}.$$ La preuve de ce fait passe par le mouvement brownien plan et le SLE($6$), mais on ne sait même pas prouver l'existence de l'exposant en n'utilisant que la marche aléatoire!
7- Retour à la marche auto-évitante
Pour en revenir au problème initial: pour la marche auto-évitante uniforme, la propriété de Markov de domaine est naturelle, mais l'invariance conforme est hors de portée; toutefois, si on la suppose vraie, on sait prouver que la limite d'échelle est un SLE($8/3$) et cela permet alors de démontrer toutes les conjectures listées plus haut et de déterminer les exposants critiques. La preuve de l'invariance conforme elle-même toutefois reste inconnue...
8- Pour en savoir plus
Le livre de Lawler [2] est une bonne introduction au SLE, et contient tous les prérequis nécessaires, à la fois en analyse complexe (pour les probabilistes) et en calcul stochastique (pour les analystes).
Références bibliographiques
[1] V. Beffara. The dimension of the SLE curves. Ann. Probab. 36, no 4 (2008), p. 1421–1452.
[2] G. F. Lawler. Conformally Invariant Processes in the Plane. 114. Mathematical Surveys and Monographs. American Mathematical Society, 2005.
[3] G. F. Lawler, O. Schramm et W. Werner. Conformal Invariance of Planar Loop-erased Random Walks and Uniform Spanning Trees ». Ann. Probab. 32, no 1B (2004), p. 939–995.
[4] G. F. Lawler, O. Schramm et W. Werner. The Dimension of the Brownian Frontier is 4/3. Math. Res. Lett. 8 (2001a), p. 13–24.
[5] G. F. Lawler, O. Schramm et W. Werner. Values of Brownian Intersection exponents I: Half-plane Exponents. Acta Mathematica 187 (2001b), p. 237–273.
[6] G. F. Lawler, O. Schramm et W. Werner. Values of Brownian Intersection exponents II: Plane Exponents. Acta Mathematica 187 (2001c), p. 275–308.
[7] P. Lévy. Processus Stochastiques et Mouvement Brownien. 2 e éd. Paris : Gauthier-Villars, 1965.
[8] K. Löwner. Untersuchungen über schlichte konforme Abbildungen des Einheitskreises. I. Math. Ann. 89, n o 1–2 (1923), p. 103–121.
[9] S. Rohde et O. Schramm. Basic properties of SLE. Ann. Math. 161, n o 2 (2005), p. 883–924. issn : 0003-486X.
[10] O. Schramm. Scaling Limits of Loop-Erased Random Walks and Uniform Spanning Trees. Israel Journal of Mathematics 118 (2000), p. 221–288
[11] S. Smirnov. Conformal invariance in random cluster models. I. Holomorphic fermions in the Ising model. Ann. Math. 172, no 2 (2010), p. 1435–1467.
[12] S. Smirnov. Critical Percolation in the Plane: Conformal Invariance, Cardy’s Formula, Scaling Limits ». C. R. Acad. Sci. Paris Sér. I Math. 333, no 3 (2001), p. 239--244.

Vincent Beffara est directeur de recherche à l'Institut Fourier de Grenoble, et spécialiste en physique statistique et probabilités.
Originellement paru dans le n°144 (avril 2015) de la Gazette.

