Raconte-moi... un groupoïde de Lie
par Stéphane Vassout
I- Introduction
Un groupoïde peut se définir de manière concise de la façon suivante : c'est une petite catégorie dans laquelle tous les morphismes sont inversibles. Cette définition pourrait laisser penser que les groupoïdes sont des objets abstraits dont l'intérêt pratique pour les mathématiciens est limité. En fait, dès leur introduction par Brandt en 1927, il apparait que ces objets mathématiques s'avèrent au contraire d'une grande utilité dans une très grande variété de champs mathématiques.
Commençons par en donner une définition plus concrète.
On appelle {groupoïde} $G$, d'espace des unités $G^{(0)}$, la donnée
des
ensembles $G$ et $G^{(0)}$ et des applications suivantes :
- $\Delta : G^{(0)}\rightarrow G$, l'application d'inclusion des unités (ou diagonale),
- une involution $i : G\rightarrow G$ appelée inversion et notée $i(\gamma)=\gamma^{-1}$,
- des applications source ($s$) et but ($r$) de $G$ dans $G^{(0)}$,
- une multiplication associative $m$ à valeurs dans $G$, définie sur l'ensemble $G^{(2)}\subset G^{2}$ des couples $(\gamma_1,\gamma_2)$ pour lesquels $r(\gamma_1)=s(\gamma_2)$,
qui vérifient les relations suivantes :
- $r(\Delta(x))=s(\Delta(x))=x$, et $m(\gamma,\Delta(s(\gamma)))=m(\Delta(r(\gamma)),\gamma)=\gamma$ ;
- $r(\gamma^{-1})=s(\gamma)$ et $m(\gamma,\gamma^{-1})=\Delta(r(\gamma)) ;$
- $s(m(\gamma_1,\gamma_2))=s(\gamma_2)$ et $r(m(\gamma_1,\gamma_2))=r(\gamma_1) ;$
- $m(\gamma_1, m(\gamma_2,\gamma_3))=m(m(\gamma_1,\gamma_2),\gamma_3)$ si $s(\gamma_1)=r(\gamma_2)$ et $s(\gamma_2)=r(\gamma_3)$.
Tout ensemble $E$ est naturellement un groupoïde (trivial, en prenant $G^{(0)}=G=E$) et est également l'ensemble des unités d'un groupoïde non trivial, appelé groupoïde des paires, où $G=E^2$ et $r$ et $s$ sont respectivement la première et la seconde projection, la multiplication étant donnée par $(x,y)(y,z)=(x,z).$
On voit facilement qu'un groupe est exactement un groupoïde dont l'ensemble des unités $G^{(0)}$ est réduit à un singleton (l'unité du groupe). Plus généralement, une famille de groupes $G_b$ indexée par un ensemble $B$ est un groupoïde d'ensemble des unités $B$, la multiplication de deux éléments n'étant définie que pour deux éléments du même groupe $G_b$, par la multiplication du groupe.
L'action d'un groupe sur un ensemble X définit également une structure de groupoïde appelée produit croisé, ce qui peut donner l'intuition qu'un groupoïde est une structure dynamique où sont présents simultanément la structure qui agit (le groupe) et l'espace sur lequel elle agit.
Les deux situations " extrêmes " sont un groupe ou une famille de groupes, ce qui correspond à $r =s$ (la composante d'espace disparaît) et le groupoïde des paires ou plus généralement le graphe d'une relation d'équivalence sur un ensemble (la composante de groupe disparaît), où l'application $(r,s)$ est une bijection sur son image.
II- Groupoïdes de Lie
Cette structure de groupoïde devient encore plus intéressante, pour traiter des problèmes mathématiques concrets, si elle est pourvue d'une structure mesurable, topologique ou différentielle adaptée. Nous allons nous concentrer essentiellement sur ce dernier cas, dont l'apparition remonte aux travaux fondateurs d'Ehresmann [7] dans les années 50, suivis par ceux de Haefliger et Pradines. Celui-ci a connu un développement très rapide dans les années 70 et 80, à la fois en raison de son intérêt pour les questions de quantification/déformation (Weinstein) et pour la géométrie non commutative développée par Alain Connes.
On appelle groupoïde de Lie un groupoïde pour lequel les ensembles $G$ et $G^{(0)}$ sont des variétés différentiables, où toutes les applications structurelles sont lisses, avec la condition que les applications source et but sont des submersions. Dans ce cas l'application $i$ est un difféomorphisme, et l'application $\Delta$ une immersion.
Tous les exemples précédents de groupoïdes fournissent des exemples de groupoïdes de Lie : le groupoïde trivial d'une variété différentiable, le groupoïde des paires sur une variété différentiable, un groupe de Lie, un fibré en groupes de Lie (en particulier un fibré vectoriel), l'action d'un groupe (ou d'un groupoïde) de Lie sur une variété différentiable, le graphe de la relation d'équivalence " être dans la même fibre" pour une fibration lisse.
Voici un exemple très naturel supplémentaire : le groupoïde de monodromie (appelé aussi groupoïde fondamental) d'une variété différentiable connexe. On considère les classes d'homotopie à extrémités fixes de chemins tracés dans $X$. Cet ensemble de chemins (à homotopie près) est muni naturellement d'une structure de groupoïde différentiable, les applications but et source étant les extrémités des chemins dans $X$, et la multiplication de deux chemins d'extrémités qui coïncident étant l'aboutement des deux chemins. Ce groupoïde contient naturellement le groupe fondamental $\Pi_1(X,x)$ pour tout point $x \in X$ comme stabilisateur du point $x$.
III- Feuilletages et groupoïdes de Lie
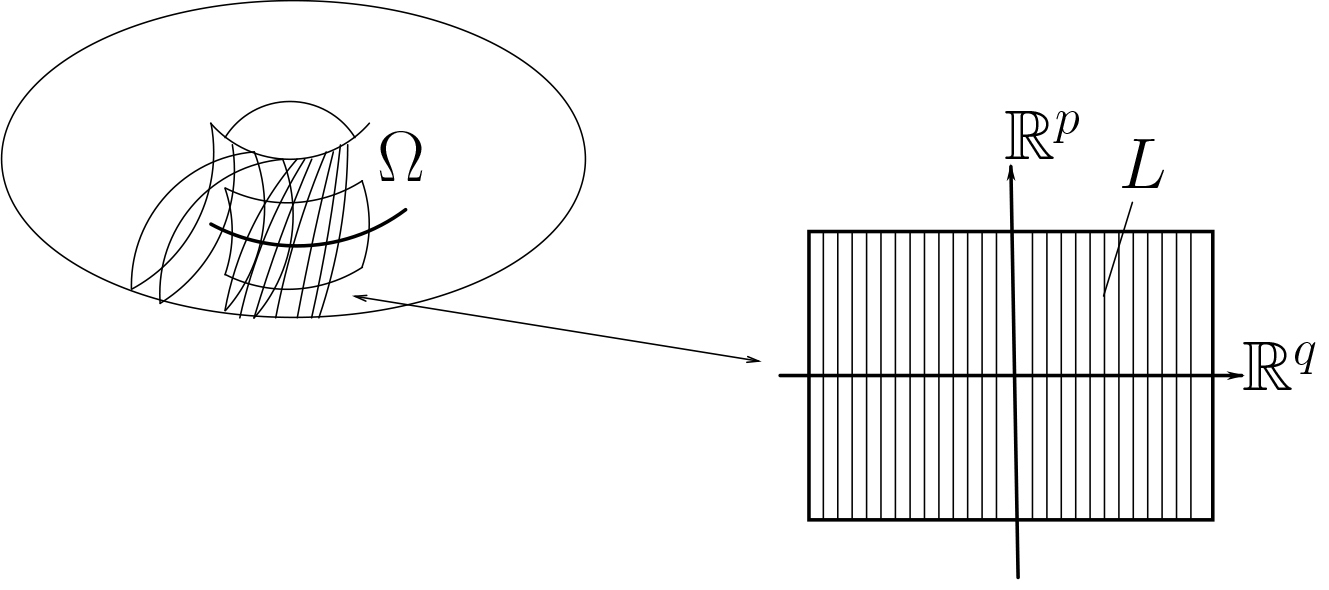
Un feuilletage régulier (de dimension $p$) est la donnée sur une variété lisse $M$ d'une relation d'équivalence dont les classes d'équivalence, appelées feuilles, sont connexes et forment une seconde structure de variété lisse (de dimension $p$) sur $M$, compatible avec la première, c'est-à-dire qu'il existe un système de cartes $\varphi : \Omega \to L\times T \subset \mathbb{R}^p\times \mathbb{R}^q$ pour $M$ pour lesquelles les composantes connexes de l'intersection de chaque feuille avec un ouvert (les plaques) sont de la forme $\varphi^{-1}(\mathbb{R}^p\times \{t\})$. Le groupoïde associé à la relation d'équivalence (" être dans la même feuille ") d'un feuilletage régulier $(M, \mathcal{F})$ ne peut pas toujours, comme dans le cas particulier d'une fibration, être muni d'une structure topologique ou différentielle consistante. On peut néanmoins toujours associer à un feuilletage un groupoïde de Lie, appelé groupoïde d'holonomie du feuilletage [9]. On peut y penser comme à un quotient du groupoïde fondamental du feuilletage (feuille à feuille) défini ci-dessus : l'ensemble des unités est $M$ et le groupoïde est l'ensemble des classes d'homotopie de chemins tracés dans une même feuille. Étant donné un chemin tracé dans une feuille, on peut le recouvrir par des ouverts de cartes du feuilletage de sorte que chaque plaque d'un ouvert intersecte au plus une plaque de l'ouvert qui suit. De cette manière, on définit en suivant le chemin une bijection d'un voisinage d'une transversale du point de départ vers un voisinage d'une transversale du point d'arrivée. Pour obtenir le groupoïde d'holonomie, il faut encore quotienter le groupoïde fondamental ci-dessus en considérant comme équivalents deux chemins qui agissent de manière identique sur le transport parallèle, le long du chemin, d'un voisinage de la transversale du point de départ vers un voisinage de la transversale du point d'arrivée. Dans ce cas, l'action naturelle du groupoïde $\mbox{Hol}(M, \mathcal{F})$ sur l'espace des unités $M$ a pour orbites exactement les feuilles du feuilletage. C'est même le groupoïde de Lie minimal vérifiant cette propriété, dans le sens que tout autre groupoïde de Lie d'espace des unités $M$ dont les orbites sont les feuilles du feuilletage admet un sous-groupoïde ouvert se projetant sur $\mbox{Hol}(M, \mathcal{F})$. Il faut noter que, dans cette construction, le groupoïde d'holonomie (la variété $G$) n'est pas nécessairement séparé.
Cette construction a été étendue par Pradines, Bigonnet, Debord au cas des feuilletages quasi-réguliers, puis plus récemment par Androulidakis et Skandalis [2] au cas de feuilletages singuliers quelconques, le prix à payer dans ce cas étant la disparition de la structure lisse globale de groupoïde de Lie.
D'un autre coté, pour tout groupoïde de Lie, les composantes connexes des orbites de l'action du groupoïde sur l'espace des unités définissent naturellement un feuilletage, en général singulier, de l'espace des unités.
IV- Groupoïdes et géométrie non commutative
Le point de départ de la géométrie non commutative est le théorème de Gelfand qui établit une bijection entre les espaces topologiques localement compacts séparés et les C$^*$-algèbres commutatives. Il donne l'idée que pour étudier un espace, on peut étudier, plutôt que l'espace lui-même, une algèbre de fonctions sur cet espace. Cette idée dépasse même le cadre topologique, puisqu'un théorème de Connes montre que la donnée d'une algèbre d'opérateurs commutative vérifiant certaines propriétés additionnelles permet de reconstruire complètement une variété riemannienne compacte. L'idée est d'appliquer cette correspondance à des espaces qui sont pathologiques vis-à-vis de la topologie ou de la géométrie ordinaire, en étudiant des C$^*$-algèbres non commutatives qui remplacent moralement les algèbres de fonctions sur l'objet pathologique.
On peut associer naturellement à chaque groupoïde topologique, en particulier aux groupoïdes de Lie, des C$^*$-algèbres [13], et le lien entre groupoïdes et géométrie non commutative se développe donc suivant deux voies.
Une première démarche est d'établir des méthodes générales, qui fournissent pour un groupoïde de Lie des outils analytiques, géométriques et topologiques permettant de construire des invariants, ou d'établir des propriétés du groupoïde au travers des algèbres d'opérateurs qui y sont associées. De nombreux progrès ont été réalisés dans cette direction depuis les années 80 : $K$-théorie et $KK$-théorie, cohomologie cyclique, algèbre des opérateurs pseudo-différentiels sur un groupoïde de Lie, théorie de l'indice...
Une direction complémentaire est de traiter des exemples géométriques concrets avec cette théorie générale. Pour ce faire, il faut pouvoir associer à un espace pathologique un groupoïde de Lie, qui constitue une désingularisation de celui-ci.
Pour reprendre l'exemple précédent, l'espace des feuilles d'un feuilletage $(M,\mathcal{F})$, c'est-à-dire le quotient de $M$ par la partition en feuilles, est en général très pathologique du point de vue de la topologie et de la géométrie ordinaire.
Dans l'exemple très simple du feuilletage de Kronecker obtenu en considérant le feuilletage du tore de dimension $2$ par des courbes de dimension $1$ de pente irrationnelle constante $\alpha$, les seules fonctions qui sont continues sur le tore et qui passent au quotient sont les fonctions constantes.
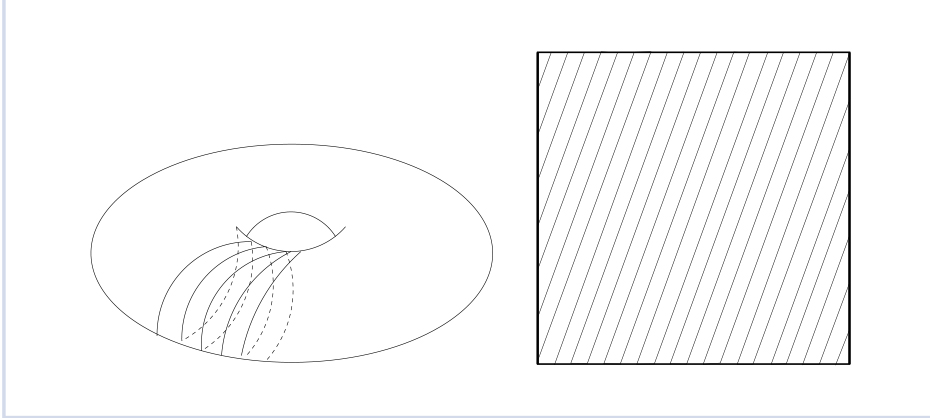
Ce fut le premier exemple de géométrie non commutative introduit par Connes et la désingularisation de cet espace est obtenue en considérant le groupoïde d'holonomie $\mbox{Hol}(M, \mathcal{F})$. La C$^*$-algèbre du groupoïde est ainsi l'algèbre se substituant naturellement à l'algèbre des fonctions continues sur l'espace des feuilles.
Depuis, de nombreux autres exemples ont enrichi la théorie : variétés à bords ou à coins [10], pseudo-variétés à singularités coniques, pseudo-variétés stratifiées,
variétés avec une structure de Lie à l'infini...
L'un des intérêts de cette approche réside dans le fait qu'une fois réalisée l'étape géométrique consistant à construire la désingularisation, les méthodes générales dont nous venons de parler sur les groupoïdes de Lie permettent naturellement d'associer de manière systématique à cette désingularisation un certain nombre d'outils analytiques et topologiques. En particulier, la question du développement d'un calcul pseudo-différentiel adapté à une situation pathologique, par exemple le $b$-calcul de Melrose pour une variété à bord, requiert généralement le développement d'une analyse raffinée sur le type de singularités considéré (par rapport au cas lisse sans bord). Elle est ici condensée simplement dans la compréhension géométrique du groupoïde de Lie associé, la théorie générale des opérateurs pseudo-différentiels sur un groupoïde de Lie étant déjà établie (dans sa thèse B. Monthubert construit un groupoïde associé à une variété à bord, et montre que le calcul pseudo-différentiel appliqué à ce groupoïde particulier est exactement le $b$-calcul de Melrose).
V- Groupoïdes de déformation
Un élément essentiel dans la compréhension des variétés lisses compactes (sans bord) est le théorème d'indice d'Atiyah et Singer démontré dans les années 60. À un opérateur différentiel ou pseudo-différentiel elliptique, on peut naturellement associer un entier, appelé indice, qui peut être défini deux manières : de façon purement analytique, ou de façon purement topologique. Le résultat d'égalité est formulé à l'aide de la $K$-théorie de la variété, et peut donc également être réinterprété en terme de la $K$-théorie de la C$^*$-algèbre commutative $C(M)$ des fonctions continues sur la variété. Un des enjeux essentiels de la géométrie non commutative est de réussir à étendre de manière appropriée ce théorème à des espaces plus singuliers, en utilisant la $K$-théorie de C$^*$-algèbres non commutatives qui tiennent le rôle de l'algèbre $C(M)$ ci-dessus.\pagebreak
Dans le développement de la théorie de l'indice dans le cadre des groupoïdes, une notion clé est celle de groupoïde de déformation : on considère deux groupoïdes de Lie $G_1$ et $G_2$ ayant même espace des unités $M$ et un recollement lisse de $G_2\times ]0,1]$ sur $G_1 \times \{0\}$ et on obtient ainsi un nouveau groupoïde de Lie, appelé groupoïde de déformation, donné par $G=G_1 \times \{0\} \cup G_2\times ]0,1]$, d'espace des unités $M\times [0,1]$. Le premier exemple d'un tel groupoïde est le groupoïde tangent d'une variété lisse compacte, introduit par Connes [4, 5] défini par le recollement de $TM \times\{0\}$ et de $M\times M\times ]0,1]$, le recollement étant fourni par :
$(x_t, y_t, t) \to (x, V,0)$ lorsque $x_t$ et $y_t$ tendent vers $x$ et $\frac{x_t-y_t}{t}$ tend vers $V$.
Cette construction permet notamment de définir l'indice analytique uniquement en termes de groupoïdes, et également de fournir une démonstration du théorème d'indice d'Atiyah-Singer utilisant uniquement les groupoïdes de déformation. La portée générale de ce type d'approche permet de démontrer, dans le même esprit, des théorèmes sur des espaces plus singuliers, comme par exemple le théorème d'indice longitudinal pour les feuilletages réguliers de Connes et Skandalis [4] ou le théorème d'indice pour les pseudo-variétés à singularité conique [3].
L'idée générale consiste à construire un groupoïde de déformation, appelé groupoïde adiabatique en remplaçant le groupoïde des paires $M \times M$ par un groupoïde de Lie $G$ et l'espace tangent à $M$ par " l'espace tangent " $AG$ naturellement associé à un groupoïde de Lie, appelé algébroïde de Lie de $G$ et qui désigne l'objet infinitésimal associé au groupoïde de Lie de la même
manière qu'une algèbre de Lie est associée à un groupe de Lie.
Plus récemment encore, Debord et Skandalis [6] ont utilisé cette notion de groupoïde adiabatique pour fournir une description du calcul pseudo-différentiel d'ordre négatif ou nul sur un groupoïde G.
Références
[1] B. AMMANN, R. LAUTER et V. NISTOR. « Pseudodifferential operators on manifolds with Lie structure at infinity ». Annals of Mathematics 165 (2007), p. 717–747.
[2] I. ANDROULIDAKIS et G. SKANDALIS. « The holonomy groupoid of a singular foliation ». J. Reine Angew. Math. 626 (2009), p. 1–37.
[3] C. DEBORD, J.-M. LESCURE et V. NISTOR. « Groupoids and an index theorem for conical pseudo-manifolds ». J. Reine Angew. Math. 628 (2009), p. 1–35.
[4] A. CONNES. Noncommutative Geometry. San Diego, CA : Academic Press, 1994.
[5] C. DEBORD et J.-M. LESCURE. « Index theory and groupoids ». In : Geometric and topological methods for quantum field theory. Cambridge Univ. Press, 2010, p. 86–158.
[6] C. DEBORD et G. SKANDALIS. «Adiabatic groupoid, crossed product by R ⇤+ and pseudodifferential calculus ». Adv. Math. 257 (2014), p. 66–91.
[7] C. EHRESMANN. Catégories et structures. Paris: Dunod, 1965, p. xvii+358.
[8] K. MACKENZIE. General theory of Lie groupoids and Lie algebroids. 213. London Mathematical Society Lecture Note Series. Cambridge: Cambridge University Press, 2005.
[9] I. MOERDIJK et J. MRUN. Introduction to foliations and Lie groupoids. 91. Cambridge Studies in Advanced Mathematics. Cambridge: Cambridge University Press, 2003, p. x+173.
[10] B. MONTHUBERT. « Groupoïdes et calcul pseudo-différentiel sur les variétés à coins». Thèse de doct. Université Paris VII-Denis Diderot, 1998.
[11] B. MONTHUBERT et F. PIERROT. « Indice analytique et groupoïde de Lie ». C.R.A.S Série 1 325 (1997), p. 193–198.
[12] V. NISTOR, A. WEINSTEIN et P. XU. « Pseudodifferential operators on differential groupoids ». Pacific J. of Math. 181, no 1 (1999), p. 117–152.
[13] J. RENAULT. A groupoid approach to C⇤-algebras. 793. Lecture Notes in Mathematics. Berlin : Springer, 1980, p. ii+160.

Stéphane Vassout
Institut de Mathématiques de Jussieu-Paris Rive Gauche. Stéphane Vassout est maître de conférences à l’université Paris Diderot, dans l’équipe d’Algèbres d’opérateurs. Ses travaux portent sur les feuilletages et les groupoïdes de Lie envisagés du point de vue de la géométrie non commutative.
Originellement paru dans le n°147 (janvier 2016) de la Gazette.

