Raconte-moi... la droite de Berkovich

par Jérôme Poineau

On appelle corps valué un corps muni d'une valeur absolue. Les exemples les plus connus sont sans doute $\mathbb{R}$ et $\mathbb{C}$ munis des valeurs absolues usuelles, mais il en existe beaucoup d'autres. Ces deux corps satisfont à une propriété supplémentaire, dite propriété d'Archimède : pour tous $y>x>0$, il existe un entier $n$ tel que $|n x| > |y|$.

On peut montrer que $\mathbb{R}$ et $\mathbb{C}$ sont les seuls corps valués archimédiens à être complets.

Dans le cas d'un corps valué $(k,|{\mkern 2mu\cdot\mkern 2mu}|)$ qui n'est pas archimédien, la valeur absolue satisfait à une version renforcée de l'inégalité triangulaire, dite ultramétrique :
\[\forall f,g\in k,\ |f+g|\le \max(|f|,|g|).\]

Comme exemple de tel corps, on peut citer le corps $\mathbb{C}(\!(t)\!)$ des séries de Laurent complexes, c'est-à-dire des séries de la forme
\[f(t) = \sum_{n\ge n_{0}} a_{n}\, t^n,\]
où $n_{0}$ est un entier relatif qui dépend de $f$. Si la série $f$ n'est pas nulle, il existe un plus grand entier $n_{0}$, appelé valuation de $f$, pour lequel la série peut s'écrire sous la forme précédente. On le note $v(f)$. On peut alors définir une valeur absolue ultramétrique $|{\mkern 2mu\cdot\mkern 2mu}|$ sur $\mathbb{C}(\!(t)\!)$ par $|0|=0$ et $|f| = 2^{-v(f)}$ pour  $f \neq 0$ ¹.

Un autre exemple classique est celui de la valeur absolue $p$-adique $|{\mkern 2mu\cdot\mkern 2mu}|_{p}$ sur $\mathbb{Q}$, où $p$ est un nombre premier. Tout nombre rationnel $a$ non nul peut s'écrire de façon unique sous la forme $\pm\, p^{n}\, \frac u v$, où $n$ est un entier relatif et $u$ et $v$ des entiers naturels non divisibles par $p$ premiers entre eux. L'entier $n$ est appelé valuation $p$-adique de $a$ et noté $v_{p}(a)$. On peut alors définir une valeur absolue ultramétrique $|{\mkern 2mu\cdot\mkern 2mu}|_{p}$ sur $\mathbb{Q}$ par $|0|=0$ et $|a|_{p} = p^{-v_{p}(a)}$  pour $a\neq 0$ ².
Nous noterons $\mathbb{Q}_{p}$ le complété de $\mathbb{Q}$ pour cette valeur absolue.

Précisons qu'un théorème d'Alexander Ostrowski assure que toute valeur absolue non triviale sur $\mathbb{Q}$ est soit la valeur absolue usuelle, soit la valeur absolue $p$-adique pour un certain nombre premier $p$ (à normalisation près). Pour étudier un problème donné sur $\mathbb{Q}$, comme l'existence d'une solution d'une équation, on perd certainement beaucoup d'information en passant à un complété fixé, par exemple $\mathbb{R}$, mais on peut espérer mieux le comprendre si l'on est capable de le traiter sur tous les complétés.

En guise de motivation pour l'étude des espaces définis sur les corps ultramétriques, ajoutons quelques mots sur un problème classique, dit problème inverse de Galois : tout groupe fini $G$ est-il groupe de Galois d'une extension finie de $\mathbb{Q}$ ? Le théorème d'irréductibilité de Hilbert assure qu'il suffit de réaliser $G$ comme groupe de Galois d'une extension finie de $\mathbb{Q}(T)$. Dans la lignée des idées exposées plus haut, il est naturel de se demander tout d'abord si une telle construction est possible pour $\mathbb{R}(T)$, ou même $\mathbb{C}(T)$, et les différents $\mathbb{Q}_{p}(T)$.

Commençons par le cas complexe. Le corps $\mathbb{C}(T)$ étant le corps des fonctions méromorphes de $\mathbb{P}^1(\mathbb{C})$, la question admet une traduction géométrique en termes de construction de revêtements, éventuellement ramifiés, de cet espace. Si l'on comprend bien la relation entre revêtements algébriques, analytiques et topologiques de $\mathbb{P}^1(\mathbb{C})$ privé d'un nombre fini de points, ce qui est le cas, on se ramène à un problème purement topologique. La description du groupe fondamental de $\mathbb{P}^1(\mathbb{C})$ privé d'un nombre fini de points comme un groupe libre permet alors d'apporter une réponse positive au problème inverse de Galois sur $\mathbb{C}(T)$, car tout groupe fini est quotient d'un groupe libre possédant suffisamment de générateurs.

Pour mettre en œuvre des arguments similaires sur $\mathbb{Q}_{p}$, il faut disposer d'espaces possédant de bonnes propriétés, proches de celles des espaces complexes. Nous expliquons dans la suite de ce texte les problèmes qui se posent et les solutions que l'on peut y apporter.

Nous ne nous attarderons pas davantage sur le problème inverse de Galois, mais souhaitons tout de même signaler que David Harbater a démontré dans [4] que l'on pouvait en effet le résoudre sur $\mathbb{Q}_{p}$. Le problème original reste cependant ouvert.

1- Topologie sur un corps ultramétrique

Les espaces classiques tels que $\mathbb{R}^n$ et $\mathbb{C}^n$ jouissent de bonnes propriétés topologiques : compacité locale, connexité par arcs locale, contractibilité locale, etc. qui tombent en défaut dans le cadre ultramétrique.

Afin d'apporter des précisions, fixons un corps valué ultramétrique complet $(k,|{\mkern 2mu\cdot\mkern 2mu}|)$. Pour $r\in \mathbb{R}^+$ et $a \in k$, notons $B(a,r)$ la boule fermée de centre $a$ et de rayon $r$. Un calcul direct montre que, pour tout point $b$ de $B(a,r)$, nous avons $B(a,r) = B(b,r)$. En d'autres termes, tout point appartenant à la boule est centre de cette boule. On en déduit que les boules fermées de rayon strictement positif sont ouvertes. Cette propriété pose inévitablement des problèmes de connexité et l'on démontre précisément que les composantes connexes de $k$ sont les points : l'espace est dit totalement discontinu.

D'autres pathologies peuvent se présenter. On vérifie, par exemple, que, lorsque $k=\mathbb{C}(\!(t)\!)$, nous avons
\[B(0,1) = \mathbb{C}[\![t]\!] = \bigsqcup_{a\in \mathbb{C}} B(a,1)^\circ,\]
où $B(a,1)^\circ$ désigne la boule unité ouverte centrée en $a$. Il s'ensuit que $B(0,1)$ n'est pas compacte et, par des arguments du même type, que $k$ n'est pas localement compact.

Il y a une vingtaine d'années, Vladimir G. Berkovich a développé dans [2] une théorie permettant de définir des espaces sur les corps ultramétriques dont les propriétés sont proches de celles des espaces réels et complexes. Ses espaces contiennent beaucoup d'autres points que ceux de $k$, dont un point appartenant à la boule fermée $B(0,1)$ mais à aucune boule ouverte de rayon 1 (rendant caducs les arguments de topologie qui précèdent). Précisons que la théorie de V. Berkovich est en réalité bien plus complète, puisqu'elle permet de définir  une géométrie analytique ultramétrique (et prolonge en cela les travaux fondateurs de John Tate des années soixante), mais nous n'aborderons pas ce point.

2-La droite de Berkovich

Soit $(k,|{\mkern 2mu\cdot\mkern 2mu}|)$ un corps valué ultramétrique complet.

 

2.1 - Définition

Ensemblistement, la droite affine au sens de Berkovich, notée ${\mathbb{A}^{1,\mathrm{an}}_{k}}$, est l'ensemble des semi-normes multiplicatives sur $k[T]$ qui induisent la valeur absolue donnée $|{\mkern 2mu\cdot\mkern 2mu}|$ sur $k$. On la munit de la topologie faible (autrement dit de la topologie la plus grossière rendant continue l'évaluation des polynômes). Montrons tout de suite qu'un point « classique », c'est-à-dire correspondant à un élément $\alpha$ de $k$, donne naturellement lieu à un point au sens de Berkovich : il suffit pour cela de considérer la semi-norme multiplicative
\[P(T) \in k[T] \mapsto |P(\alpha)| \in \mathbb{R}_{+}.\]
Dans la suite du texte, nous noterons encore $\alpha$ ce point.

Il est possible de généraliser la construction précédente en considérant non plus seulement des éléments de $k$, mais aussi d'un corps valué complet arbitraire $K$ contenant $k$ et dont la valeur absolue étend celle de $k$. Tout point de la droite de Berkovich peut d'ailleurs s'obtenir de la sorte.

Nous disposons donc de deux définitions de la droite de Berkovich. Si la première, en termes de semi-normes multiplicatives, est plus concrète et permet de parvenir à une description explicite de la droite, la seconde, en termes de points à valeurs dans des corps valués, peut sembler plus naturelle et présente en outre un intérêt théorique certain. Elle doit rappeler la construction classique de Gelfand du spectre d'une algèbre de Banach complexe à partir des caractères de cette algèbre. Il est remarquable que les propriétés connues de ce spectre restent valables ici : l'espace $\mathbb{E}{1}{k}$ est séparé et localement compact³, bien que le corps $k$ lui-même ne satisfasse pas toujours à cette dernière propriété.

2.2- Un nouveau point

Soit $P(T) = \sum_{i=0}^d p_{i}\, T^i$ un polynôme à coefficients dans $k$. Dans le cadre ultramétrique, le supremum de sa valeur absolue sur le disque $B(0,1)$ est donné explicitement par
\[ \|P\|_{\infty,B(0,1)} = \max_{0\le i\le d}(|p_{i}|). \]
On peut alors vérifier que l'application
\[P \in k[T] \mapsto \|P\|_{\infty,B(0,1)}  \in \mathbb{R}_{+}\]
est une norme multiplicative sur $k[T]$. Insistons sur le fait que cette propriété est très spécifique au cadre ultramétrique et que la norme du supremum sur un disque complexe n'est nullement multiplicative.

La norme multiplicative précédente définit un point de $\mathbb{E}{1}{k}$, souvent appelé point de Gauss, que nous noterons $\eta$. Il est loisible d'y penser comme à une sorte de point générique du disque unité fermé (ou du cercle unité) centré en 0. Il appartient en effet à la boule fermée de centre 0 et de rayon 1 (puisque $\|T\|_{\infty,B(0,1)}=1$) mais à aucune boule ouverte de centre $a$, avec $|a|\le 1$, et de rayon 1 (puisque $\|T-a\|_{\infty,B(0,1)}=1$).

Énonçons un autre résultat pour étayer cette idée de généricité. Soit $(x_{n})_{n\in\mathbb{N}}$ une suite de racines de l'unité dont l'ordre tend vers l'infini. Pour tout entier $n$, notons $X_{n}$ l'ensemble des conjugués du point $x_{n}$ et considérons la mesure de probabilité sur $\mathbb{C}$ définie par
\[\delta_{n} = \frac{1}{\sharp X_{n}}\, \sum_{y\in X_{n}} \delta_{y},\]
où $\delta_{y}$ désigne la mesure de Dirac au point $y$. On vérifie que les éléments des $X_{n}$ s'équirépartissent sur le cercle unité, au sens où la suite de mesures $(\delta_{n})_{n\in\mathbb{N}}$ converge faiblement vers la mesure de Haar sur ce cercle (cf. [7], où les auteurs traitent des cas bien plus généraux).

 

Soit $p$ un nombre premier. On peut effectuer une construction similaire à la précédente sur la droite de Berkovich $\mathbb{E}{1}{\mathbb{Q}_{p}}$ sur $\mathbb{Q}_{p}$ et associer à la suite $(x_{n})_{n\in\mathbb{N}}$ une suite de mesures $(\delta_{n})_{n\in\mathbb{N}}$. Dans ce cas, Antoine Chambert-Loir a montré dans [3] que cette suite convergeait faiblement vers $\delta_{\eta}$, la mesure de Dirac au point de Gauss (ainsi que de vastes généralisations, dans l'esprit de [7]).

Ce dernier résultat rend tangible l'intérêt des espaces de Berkovich pour au moins deux raisons :

1. les points nouveaux, tel $\eta$, peuvent apparaître naturellement même dans des questions qui concernent a priori seulement des points dans des extensions finies du corps de base (ici $\mathbb{Q}_{p}$) ;
2. la compacité locale de l'espace permet d'utiliser le fait que l'ensemble des mesures de probabilité sur un espace compact et métrisable est compact (pour la topologie vague).
    

2.3- Beaucoup de nouveaux points

La construction du point $\eta$ se généralise de la façon suivante. Fixons un élément $\alpha$ de $k$ et un nombre réel $r$ strictement positif. Nous pouvons écrire tout polynôme dans la base des puissances de $T-\alpha$ et définir ainsi une application
\[P(T) = \sum_{i=0}^d p_{i}\, (T-\alpha)^i \in k[T] \mapsto \max_{0\le i\le d}(|p_{i}| r^i) \in \mathbb{R}_{+}\]
qui est encore une norme multiplicative sur $k[T]$. Nous noterons $\eta_{\alpha,r}$ le point de $\mathbb{E}{1}{k}$ associé. On vérifie qu'il dépend uniquement du disque de centre $\alpha$ et de rayon $r$ (dans toutes les extensions valuées de $k$). En particulier, si $|\beta-\alpha|\le r$, alors $B(\alpha,r) = B(\beta,r)$ et $\eta_{\alpha,r} = \eta_{\beta,r}$.

En utilisant cette construction, on voit naturellement apparaître des intervalles réels tracés sur la droite de Berkovich, par exemple $\{\eta_{\alpha,r} \mid r \in\mathbb{R}^+\}$, où l'on a identifié $\eta_{\alpha,0}$ à $\alpha$. Remarquons que les intervalles issus de deux points $\alpha$ et $\beta$ de $k$ ne sont jamais disjoints car les points $\eta_{\alpha,|\alpha-\beta|}$ et $\eta_{\beta,|\alpha-\beta|}$ co\"{\i}ncident ! La construction de Berkovich permet donc de tracer un chemin entre les points $\alpha$ et $\beta$ et d'obtenir des propriétés de connexité par arcs pour $\mathbb{E}{1}{k}$ alors que, rappelons-le, le corps $k$ lui-même est totalement discontinu.

En traçant les chemins partant de tous les points de $k$, nous obtenons un dessin qui présente l'aspect suivant.

 

 

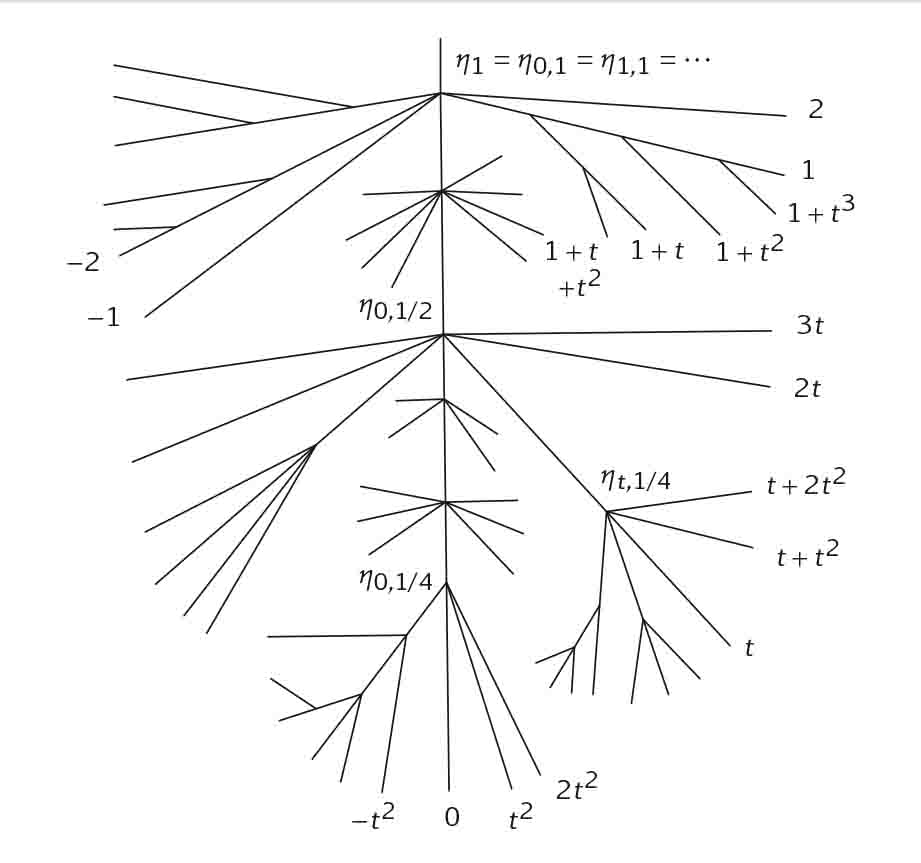
Nous obtenons un espace avec une structure d'arbre réel où les points de branchements sont denses dans tous les intervalles et où une infinité de branches partent de chaque point de branchement (sauf dans le cas où la valeur absolue sur $k$ est triviale). Remarquons que les points de branchement correspondent exactement aux plus petits disques contenant deux éléments distincts de $k$. Leur rayon doit donc être égal à la distance entre deux éléments, et donc appartenir à $|k^\ast|$.

Nous supposerons désormais que le corps $k$ est algébriquement clos. Dans ce cadre, V. Berkovich a introduit la terminologie suivante :

• un point de la forme $\eta_{\alpha,0} = \alpha$, avec $\alpha\in k$, est dit de type 1 ;
• un point de la forme $\eta_{\alpha,r}$, avec $\alpha\in k$ et $r\in |k^\ast|$, est dit de type 2 ;
• un point de la forme $\eta_{\alpha,r}$, avec $\alpha\in k$ et $r\notin |k^\ast|$, est dit de type 3.
   

La classification n'est pas encore complète car il reste un type de points que nous n'avons pas décrit. Leur construction s'appuie sur la remarque cruciale que la borne inférieure d'une famille décroissante de semi-normes multiplicatives sur $k[T]$ est encore une semi-norme multiplicative. Si cette famille est associée à une famille de disques, alors la semi-norme limite devrait correspondre à leur intersection. Cependant, dans un contexte ultramétrique où les disques fermés peuvent ne pas être compacts, une telle intersection peut être vide. Il en subsiste néanmoins une trace dans l'espace de Berkovich : un point, dit de type 4. Ces points se situent au bout de certaines branches de l'arbre et l'on ne peut les omettre sous peine de perdre la compacité locale de l'espace.

Il est frappant de constater que les points de type 4, qui sont les plus difficiles à se représenter et à étudier, présentent finalement un comportement très simple. Par exemple, la valeur absolue d'un polynôme est toujours constante au voisinage d'un tel point.

3- Espaces de Berkovich de dimension supérieure

Soit $(k,|{\mkern 2mu\cdot\mkern 2mu}|)$ un corps valué ultramétrique complet. En considérant des ensembles de semi-normes multiplicatives non plus sur $k[T]$, mais sur $k[T_{1},\dotsc,T_{n}]$, où $n$ est un entier, on obtient l'espace affine de dimension $n$ au sens de Berkovich. On peut alors définir des espaces plus généraux en considérant des fermés analytiques de ceux-ci (ou de leurs boules), puis des recollements de ces derniers. Les propriétés de compacité locale et de connexité par arcs locale que nous avons mentionnées pour la droite restent valables dans ce cadre étendu.

En dimension supérieure à 2, les espaces échappent à toute description explicite. On peut encore définir des points « génériques » de disques et même de parties plus compliquées (données par des inégalités entre polynômes), mais ceux-ci ne recouvrent qu'une petite partie des espaces, de plus en plus limitée au fur et à mesure que la dimension croît. Il est cependant remarquable que ces points contiennent une large part de l'information topologique. Par exemple, dans leurs travaux sur la contractibilité locale des espaces, Berkovich (cf. [1]) et Hrushovski-Loeser (cf. [5]) rétractent localement les espaces sur des sous-ensembles, homéomorphes à des complexes simpliciaux, qui sont formés de points génériques.

D'autre part, ces points génériques permettent également de réaliser différentes constructions combinatoires à l'intérieur des espaces de Berkovich. Le prototype de ce genre d'idées consiste à plonger $\of{]}{0,1}{[}^n$  dans $\mathbb{E}{n}{k}$ en envoyant $(r_{1},\dotsc,r_{n})$ sur le point générique de la boule de centre 0 et de poly-rayon $(r_{1},\dotsc,r_{n})$. On peut ainsi plonger l'éventail d'une variété torique dans l'espace de Berkovich associé à cette variété (cf. [8]), l'immeuble de Bruhat-Tits d'un groupe réductif dans l'espace de Berkovich associé à ce groupe (cf. [2] et [6]), etc.

 

Références

[1] V. G. BERKOVICH. « Smooth p-adic analytic spaces are locally contractible ». Invent. Math. 137, no 1 (1999), p. 1–84.

[2] V. G. BERKOVICH. Spectral theory and analytic geometry over non-Archimedean fields. 33. Mathematical Surveys and Monographs. American Mathematical Society, Providence, RI, 1990, p. x+169.

[3] A. CHAMBERT-LOIR. « Mesures et équidistribution sur les espaces de Berkovich ». J. Reine Angew. Math. 595 (2006), p. 215–235.

[4] D. HARBATER. « Galois coverings of the arithmetic line ». In : Number theory (New York, 1984–1985). Vol. 1240. Lecture Notes in Math. Springer, Berlin, 1987, p. 165–195.

[5] E. HRUSHOVSkI et F. LOESER. « Non-archimedean tame topology and stably dominated types». Annals ofMathematics Studies 192 (sept. 2016).

[6] B. RÉMY, A. THUILLiER et A. WERNER. « Bruhat-Tits theory from Berkovich’s point ofview. I. Realizations and compactifications of buildings». Ann. Sci. Éc. Norm. Supér. (4) 43, no 3 (2010), p. 461–554.

[7] L. SZPIRO, E. ULLMO et S. ZHANG. « Èquirépartition des petits points». Invent. Math. 127, no 2 (1997), p. 337–347.

[8] A. THUILLIER. « Géométrie toroïdale et géométrie analytique non archimédienne. Application au type d’homotopie de certains schémas formels». Manuscripta Math. 123, no 4 (2007), p. 381–451.

 

 

1- La constante $2$ est choisie arbitrairement et pourrait être remplacée par n'importe quel nombre réel strictement supérieur à 1.
Université de Caen Normandie

2- Ici aussi, la constante $p$ que l'on élève à la puissance $v_{p}(a)$ peut être modifiée. Ce choix particulier est cependant intéressant en ce qu'il conduit à la formule du produit : pour tout nombre rationnel non nul $a$, on a $|a| \prod_{p} |a|_{p} = 1$, où $p$ parcourt l'ensemble des nombres premiers.

3- Il serait compact si l'on avait considéré plutôt des disques, c'est-à-dire si l'on avait imposé des bornes aux valeurs prises par les semi-normes sur des fonctions coordonnées.

 

 

 

Originellement paru dans le n°148 (avril 2016) de la Gazette.