Raconte-moi... une orbite de Reeb
par Anne Vaugon
I- Un peu de mécanique hamiltonienne
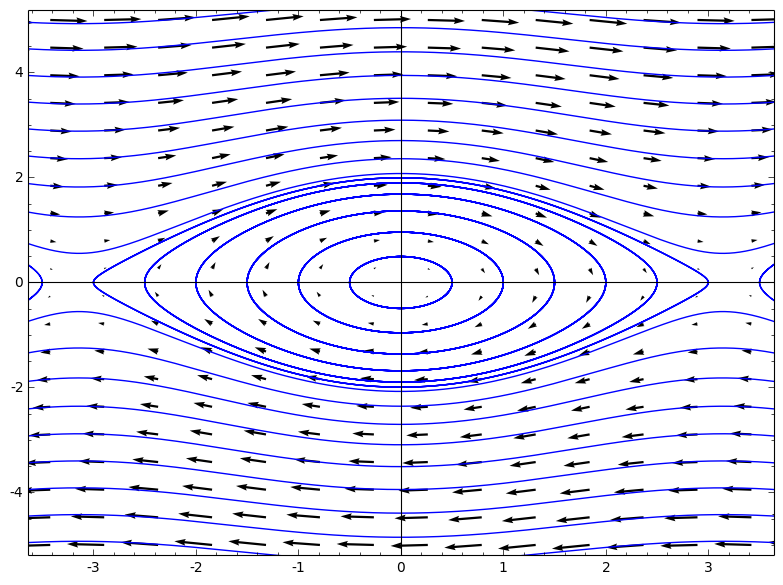
Considérons un pendule simple de masse $m$ et de longueur $l$. Repérons sa position par l'angle $x$ qu'il forme avec la verticale et notons $y$ son impulsion. L'énergie $H$ du pendule s'obtient en ajoutant son énergie cinétique et son énergie potentielle, soit $H(x,y)=\frac{1}{2m} y^2-mgl\cos(x)$. Son mouvement est décrit par le système différentiel
\[
\left\{
\begin{array}{l}
\dot{x}=\frac{y}{m}\\
\dot{y}=-mgl\sin(x)
\end{array}
\right.
\]
ou, de façon équivalente, par le champ de vecteurs $X_H=\left(\frac{y}{m},-mgl\sin(x)\right)$. Une trajectoire dans l'espace des phases est alors une courbe $t\mapsto (x(t), y(t))$ dont le vecteur vitesse en tout point est un vecteur de $X_H$.
La figure~1 représente le champ de vecteurs et des trajectoires du pendule simple.
Cette description correspond au formalisme hamiltonien de la mécanique classique qui s'applique dans un cadre très général, des problèmes de pendule à la mécanique céleste. Dans le cas le plus simple, un système est alors repéré par les coordonnées $(x,y)\in\mathbb R^{2n}$ où $x\in \mathbb R^n$ représente la position et $y\in\mathbb R^n$ l'impulsion. Son évolution est décrite grâce à une fonction lisse $H: \mathbb R^{2n}\to\mathbb R$ appelée hamiltonien via l'équation différentielle
\[
\left\{
\begin{array}{l}
\dot{x}=\frac{\partial H}{\partial y}\\
\dot{y}=-\frac{\partial H}{\partial x}
\end{array}
\right. .
\]
Les solutions peuvent également être interprétées comme les orbites associées au champ de vecteurs $X_H=\left(\frac{\partial H}{\partial y}, -\frac{\partial H}{\partial x}\right)$.
Au cours du mouvement le hamiltonien $H$ est préservé et on restreint souvent l'étude à un niveau régulier de $H$ qui est alors une hypersurface de $\mathbb R^{2n}$. C'est ce que nous allons faire ici.
Dans le cas du pendule simple, les niveaux sont de dimension $1$. Pour obtenir des propriétés dynamiques intéressantes sur les niveaux de $H$, il faut regarder des systèmes en dimension plus grande.
Considérons donc un exemple explicite d'oscillations en dimension $2$ obtenu à l'aide de deux systèmes masse-ressort indépendants et de fréquences propres respectives $1$ et $\omega$ herz. Le hamiltonien $H : \mathbb R^4\to \mathbb R$ est alors donné par la formule
\[H(x_1,x_2,y_1,y_2)=\frac{1}{2}\left(x_1^2+\omega^2 x_2^2\right)+\frac{1}{2}\left(y_1^2+y_2^2\right) \]
et s'obtient en sommant les énergies cinétique et potentielle.
Si $\omega=1$, on retrouve également l'approximation associée aux petites oscillations d'un pendule sphérique.
Il est ici possible de résoudre explicitement l'équation différentielle associée à $H$.
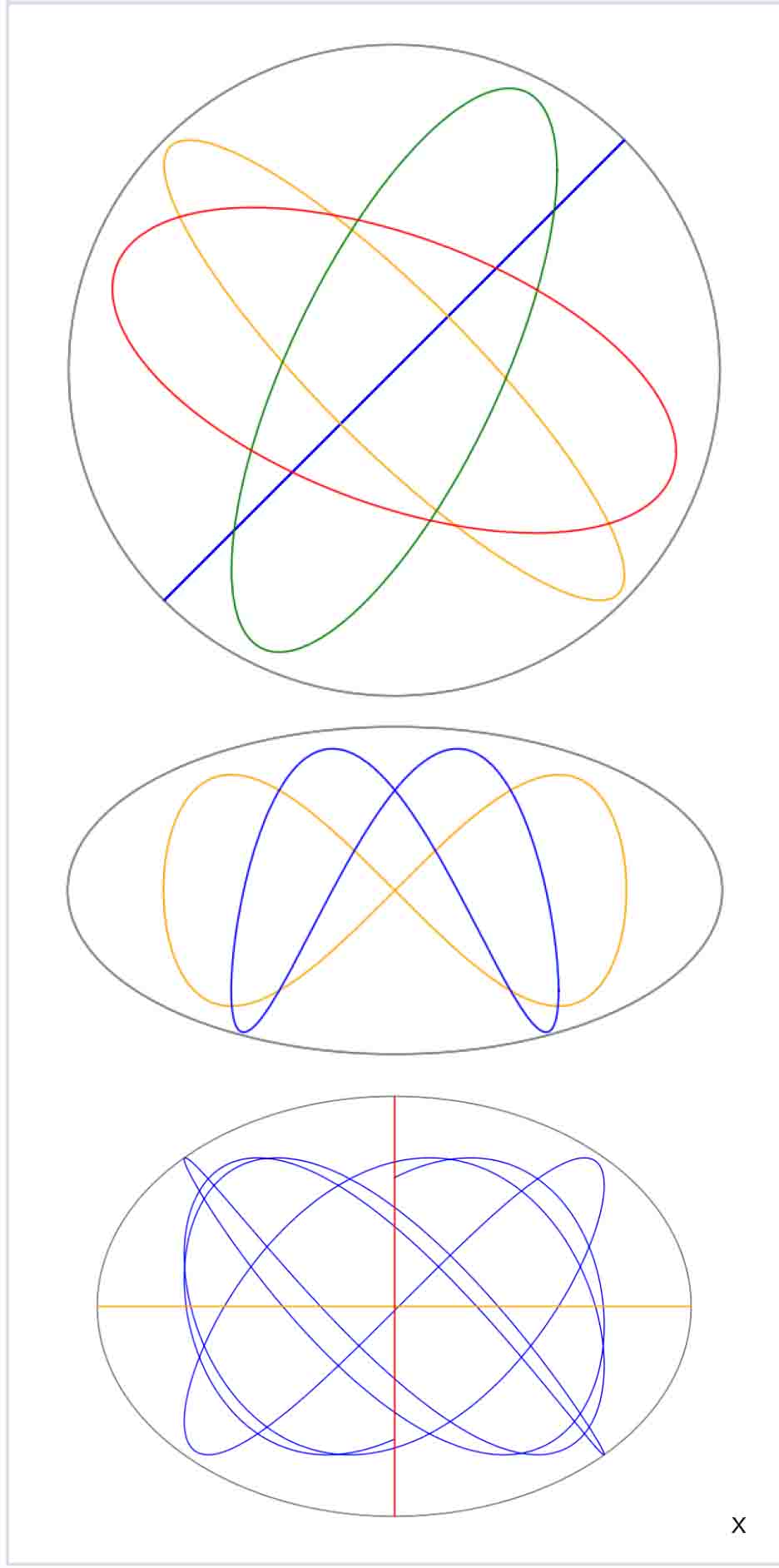
Une solution projetée sur les coordonnées $(x_1,x_2)$ est une courbe de Lissajous, c'est-à-dire une courbe paramétrée de la forme
\[
\left\{
\begin{array}{l}
x_1(t)=a_1\sin(t+\phi_1)\\
x_2(t)=a_2\sin(\omega t+\phi_2)
\end{array}
\right.
\]
où $a_1$, $a_2$, $\phi_1$ et $\phi_2$ sont des réels. Une solution est contenue dans l'ellipsoïde $H^{-1}(c)$ où $c=\frac{1}{2}a_1^2+\frac{1}{2}\omega^2 a_2^2$. Sa projection sur les coordonnées $(x_1,x_2)$ est donc à l'intérieur de l'ellipse d'équation $x_1^2+\omega^2 x_2^2=2c$ (en gris sur les figures). Lorsque $\omega$ est rationnel, toutes les trajectoires sur un niveau régulier de $H$ sont périodiques. Si $\omega$ est irrationnel, il y a exactement deux trajectoires périodiques vérifiant respectivement $x_1=0$ et $x_2=0$ (voir figure~2).
Le procédé décrit ici n'est pas limité à $\mathbb R^n$ et on peut construire un champ de vecteurs à partir d'une fonction hamiltonienne dès que notre variété est munie d'une structure géométrique appelée structure symplectique.
Le flot géodésique peut être interprété dans ce cadre, c'est un exemple fondamental de flot hamiltonien.
Considérons une surface $S$ (ou, plus généralement, une variété de dimension quelconque) munie d'une métrique riemannienne, c'est-à-dire d'un produit scalaire $\langle \cdot,\cdot\rangle$ sur chaque espace tangent. Les courbes qui minimisent localement la distance sont appelées géodésiques.
Ce sont les trajectoires associées au hamiltonien
\[H(x,v)=\frac{1}{2}\langle v,v\rangle \]
défini sur le fibré tangent de $S$, c'est-à-dire l'ensemble des vecteurs tangents à $S$. Choisir un niveau de $H$ revient à choisir la vitesse des géodésiques. Les orbites périodiques correspondent aux géodésiques fermées.
II- À la recherche des orbites périodiques
Il est en général délicat d'étudier les orbites associées à un hamiltonien. Pour dire quelque chose sur les propriétés dynamiques du flot hamiltonien, on s'intéresse aux orbites périodiques. C'est Henri Poincaré qui a introduit cet angle d'approche de la dynamique dans ses travaux sur la mécanique céleste : il démontre l'existence d'orbites périodiques pour le problème à trois corps et peut alors obtenir des informations sur la dynamique au voisinage de ces orbites.
On se pose donc le problème suivant. Soit $H:\mathbb R^n\to\mathbb R$ et $c$ une valeur régulière de $H$. Existe-t-il toujours une trajectoire périodique sur $S=H^{-1}(c)$ ? En général non (Ginzburg et Herman ont construit de tels exemples) mais on peut répondre positivement à cette question dans certains cas.
Tout d'abord, les trajectoires périodiques de certains flots hamiltoniens particuliers, comme les flots géodésiques, ont fait l'objet de nombreux travaux spécifiques. Ainsi les travaux, entre autres, d'Hadamard en 1898 de Lyusternik et Fet en 1951 ont permis de garantir l'existence de géodésiques fermées dans le cas général (pour une variété compacte sans bord).
Les premières avancées concernant l'existence d'orbites périodiques dans le cas général datent de Rabinowitz et Weinstein en 1978.
En 1987, Viterbo [12] a prouvé l'existence d'une orbite périodique sous des hypothèses beaucoup plus satisfaisantes en considérant des hypersurfaces particulières dites de type contact. Dans ce cas, l'hypersurface $S$ est en fait une variété de contact et le champ hamiltonien est le champ de Reeb associé. Tous les exemples précédents rentrent dans ce cadre.
III- Champs de Reeb
Certains champs de Reeb sont donc des champs hamiltoniens sur des hypersurfaces de $\mathbb R^{2n}$ mais ce champ de vecteurs est défini dans un cadre plus général et plus intrinsèque.
Il est maintenant temps de donner cette définition générale.
Formellement, une $1$-forme $\alpha$ sur une variété de dimension $3$ (on peut en fait donner une définition en toute dimension impaire) est dite de contact s'il existe, au voisinage de tout point, des coordonnées $(x,y,z)$ dans lesquelles $\alpha=d z -y d x$. Dans ces coordonnées, le champ de Reeb est le champ $\frac{\partial}{\partial z}$. Plus intrinsèquement, le champ de Reeb $R$ est décrit par les équations $\alpha(R)=1$ et $d\alpha(R,\cdot)=0$.
À la différence des structures riemanniennes, par exemple, toutes les formes de contact sont donc les mêmes localement.
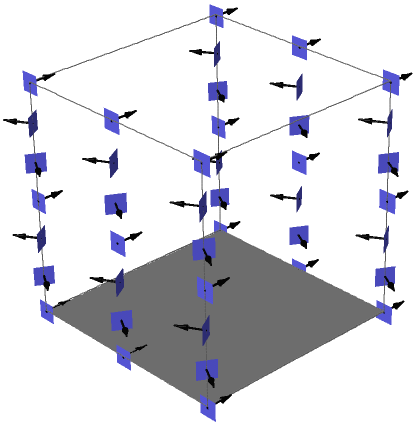
Cette définition nous cache beaucoup de choses : en particulier l'objet géométrique fondamental est ici le noyau de $\alpha$, c'est-à-dire le champ de plans dont le modèle en coordonnées locales est représenté sur la figure 3. On parle alors de structure de contact.

à la forme $\alpha=d z -y dx$ (en bleu) et champ de Reeb (en noir)
L'étude des structures de contact date des travaux de Sophus Lie sur les équations différentielles. La géométrie de contact puise son inspiration dans la mécanique classique, l'optique géométrique et la thermodynamique.
Plus spécifiquement, l'étude des champs de Reeb a été introduite par Georges Reeb [10] à la suite des travaux d'Elie Cartan sur les invariants intégraux.
Les structures de contact existent sur toutes les variétés de dimension $3$ compactes sans bord. On a vu qu'elles apparaissaient naturellement sur certaines surfaces de niveau d'un hamiltonien. Plus généralement, une structure de contact est ce qui reste d'une variété symplectique sur son bord s'il est assez \enquote{joli} : une forme de contact est alors donnée par la restriction d'une primitive de la forme symplectique. Savoir si une structure de contact est le bord d'une variété symplectique est une question fondamentale en topologie de contact.
Les exemples présentés dans la première section nous fournissent des exemples de variétés de contact et de champs de Reeb.
L'exemple de l'oscillateur dans le cas $\omega=1$ nous donne une forme de contact sur $S^3$ dont le flot de Reeb n'a que des orbites périodiques (ce sont les fibres de la fibration de Hopf). Dans le cas du flot géodésique, on obtient une forme de contact sur le fibré unitaire tangent d'une surface (c'est-à-dire l'ensemble des vecteurs tangents de norme~$1$) dont le flot de Reeb est le flot géodésique.
associée à la forme $\alpha=\cos(z) d x - \sin(z) d y$ (en bleu)
et champ de Reeb (en noir).]
Détaillons un peu ce qui se passe dans le cas du flot géodésique sur le tore plat $T^2$ (voir figure 4).
Le fibré unitaire tangent est alors $T^2\times S^1$ qui n'est autre que le tore en trois dimensions. Si on repère un point par les coordonnées $(x,y,z)$, on obtient comme forme de contact
$\alpha=\cos(z) d x - \sin(z) d y$.
Le champ de Reeb a alors pour coordonnées $(\cos(z),-\sin(z),0)$, il est tangent aux tores $T_z$ obtenus en fixant la coordonnée $z$ (voir figure 5). Ses trajectoires sont les géodésiques, ici des droites. La pente de la droite est donnée par la coordonnée $z$. Si la pente est rationnelle, le tore $T_z$ est feuilleté par des orbites périodiques (voir figure 6 et si la pente est irrationnelle, les orbites sont denses dans le tore $T_z$.
Dans le cas d'une surface hyperbolique la situation est très différente : il y a exactement une orbite fermée par classe d'homotopie libre de la surface (et il y a beaucoup de telles classes).
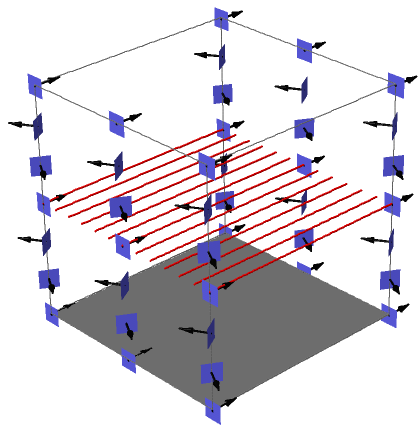
avec quelques orbites de Reeb sur $T_{\pi}$ (en rouge)
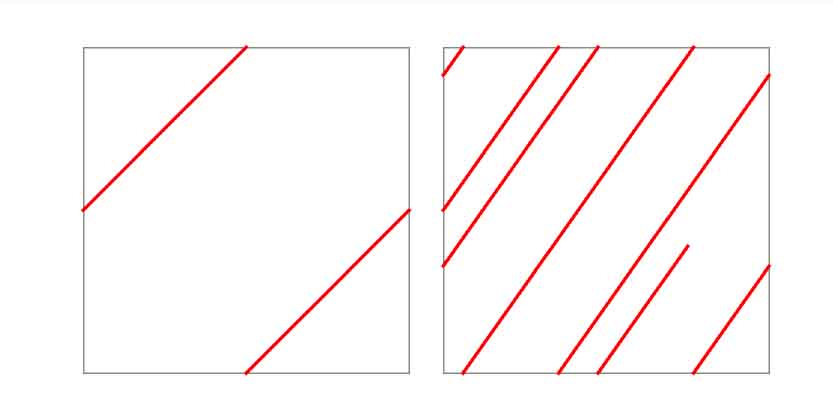
et irrationnelle (à droite) sur des tores $T_z$
Pour conclure cette série d'exemples, la figure 7 décrit une autre structure de contact sur $\mathbb R^3$ de forme de contact $\alpha=\cos(r)d z+ r\sin(r) d \theta$ en coordonnées polaires. Elle appartient à la classe des structures dite vrillées. Distinguer ce type de structure a été le premier pas fondamental vers l'étude des structures de contact en dimension $3$. Les travaux de Bennequin et Eliashberg jouent ici un rôle déterminant. Trouver des équivalents en dimension supérieure est actuellement un sujet très actif.

sur $\mathbb R^3$ associée à $\alpha=\cos(r)d z+ r\sin(r) d \theta$
Revenons aux propriétés dynamiques des champs de Reeb.
Tous les champs de Reeb ne proviennent pas de champs hamiltoniens mais la propriété dynamique remarquable des champs hamiltoniens sur les hypersurfaces de contact est préservée : tout champ de Reeb sur une variété compacte sans bord de dimension $3$ admet une orbite périodique.
Cette propriété a été formulée par Weinstein en 1979 dans le cadre hamiltonien. Elle a finalement été démontrée par Taubes [11] en 2007. Sa preuve, très délicate, repose sur des techniques analytiques nouvelles : la théorie de Seiberg-Witten. La conjecture de Weinstein est toujours ouverte en dimension supérieure. Les structures de contact sont alors moins bien comprises qu'en dimension $3$ même s'il y a eu récemment de très grandes avancées concernant l'existence de telles structures.
L'étude de la conjecture de Weinstein a permis d'introduire des techniques fascinantes en topologie de contact. Ainsi Hofer [5] a développé l'utilisation des courbes holomorphes pour démontrer l'existence d'une orbite périodique de Reeb contractile pour les structures vrillées en s'inspirant des travaux de Gromov en géométrie symplectique.
Les orbites périodiques des champs de Reeb sont également à la base de nouveaux invariants définis dans l'esprit des homologies de Morse et Floer et introduits par Eliashberg, Givental et Hofer. Ces invariants jouent un rôle prépondérant dans l'étude actuelle de la topologie de contact.
Il reste encore beaucoup à apprendre sur les propriétés dynamiques des champs de Reeb.
Par exemple, la conjecture de Weinstein garantit l'existence d'une orbite périodique de Reeb, peut-on obtenir une meilleure minoration en fonction de la topologie de la variété ?
Que peut-on dire des classes d'homotopie des orbites périodiques ?
Quel est le comportement asymptotique avec $T$ du nombre d'orbites périodiques de période inférieure à $T$ ?
Comment peut-on relier les propriétés dynamiques des champs de Reeb aux propriétés géométriques de la variété sous-jacente ?
IV- Pour en savoir plus
Les articles de J. Buzzi [2] et P. Massot [9] sur le site \emph{Image des mathématiques} permettent d'en apprendre plus sur Hadamard et les géodésiques fermées et sur la géométrie de contact.
La page web de P. Massot contient également de belles illustrations et explications sur le sujet.
Le formalisme hamiltonien de la mécanique classique est expliqué en détail dans le livre de V.I. Arnold [1].
L'article de H. Geiges [3] présente la géométrie de contact d'un point de vue historique et l'ouvrage [4] d'un point de vue théorique.
Les aspects historiques sont également présentés par R. Lutz dans l'article [8] (un petit peu difficile à trouver).
On pourra consulter [7] pour plus d'informations sur les géodésiques fermées et [6] pour plus de détails sur la dynamique hamiltonienne.
Références
[1] V. I. ARNOLD. Mathematical Methods of Classical Mechanics. Springer-Verlag, 1989.
[2] J. BUzzI. Hadamard et les systèmes dynamiques. Images des Mathématiques, CNRS. 2013.
[3] H. GEIGES. « A Brief History of Contact Geometry and Topology ». Expo. Math. 19 (2001), p. 25–53.
[4] H. GEIGES. An Introduction to Contact Topology. Cambrige University Press, 2008.
[5] H. HOFER. « Pseudoholomorphic curves in symplectisations with applications to the Weinstein conjecture in dimension 3 ». Invent. Math 114 (1993), p. 515–565.
[6] H. HOFER et E. ZEHNDER. Symplectic invariants and Hamiltonian dynamics. Birkhâuser, 2012.
[7] W. KLINGENBERG. Lectures on Closed Geodesics. Springer, 1978.
[8] R. LUTz. « Quelques remarques historiques et prospectives sur la géométrie de contact ». Rend. Sem. Fac. Sci. Univ. Cagliari 58 (1988). Conference on Differential Geometry and Topology, p. 361–393.
[9] P. MASSOT. Le théorème de Bennequin I et II. Images des Mathématiques, CNRS. 2010.
[10] G. REEB. « Sur certaines propriétés topologiques des trajectoires des systèmes dynamiques». Acad. Roy. Belgique. Cl. Sci. Mém. 27, no 9 (1952).
[11] C. H. TAUBES. « The Seiberg-Witten equations and the Weinstein conjecture». Geom. Topol. 11 (2007), p. 2117–2202.
[12] C. VITERBO. « A proof ofWeinstein conjecture in R2n». Ann. Inst. H. Poincaré, Anal. non linéaire 4 (1987), p. 337–356.

Anne Vaugon
Laboratoire de mathématiques, UMR 8628, université Paris-Sud, Orsay.
Anne Vaugon est maître de conférences. Elle travaille en géométrie symplectique et en dynamique et s'intéresse plus particulièrement à la géométrie de contact.
Originellement paru dans le n°146 (octobre 2015) de la Gazette.

