"Leonhard Euler, ou l'art de donner un sens à ce qui n'en avait pas"
par Jean-Pierre Ramis
Accéder à la vidéo
Rien de plus simple, en apparence, que d'étudier une somme d'une infinité de nombres, telle que les sommes 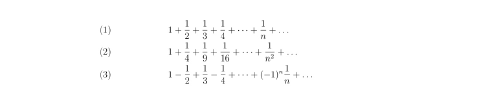
C'est en réalité un problème difficile, que les Grecs n'avaient pas les moyens d'appréhender; et ce n'est qu'à partir du XVIIème siècle qu'on a pu comprendre que
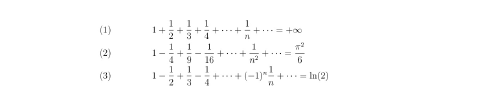
formules dont la démonstration demande une certaine connaissance des mathématiques. Le point commun de ces trois sommes est qu'on additionne des termes qui deviennent de plus en plus petits : en additionnant chaque terme supplémentaire, la somme se modifie de moins en moins. Curieusement, le résultat est très différent puisque la première somme est le nombre « infini », alors que les autres donnent un résultat fini. Mais les mathématiciens se sont tout de suite posés des questions bien plus étranges, telles que donner un sens à des sommes où on additionne ou soustrait des termes qui ne deviennent pas très petits, voire qui sont de plus en plus grands, comme :
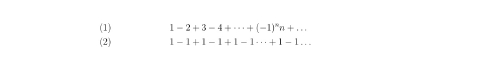
C'est à cette question que le grand mathématicien suisse Leonhard Euler s'intéresse dans son article de 1746 : quel sens donner à ces sommes... qui n'en ont pas. Donner un sens à ce qui n'en a pas : démarche permanente des mathématiciens, dont on verra ici un étonnant exemple, et surtout un héritage qui nous mènera aux recherches en mathématiques et en physique les plus contemporaines .
L. Euler, De seriebus divergentibus (1746) Opera Omnia, I, 14, 585-617
Jean-Pierre Ramis, ancien élève de l'Ecole normale supérieure, a été au CNRS et professeur aux l'universités de Tunis, Paris et Strasbourg avant de rejoindre l'université Paul Sabatier à Toulouse en 1994. Il est membre senior de l'institut universitaire de France depuis 1996, et a été élu à l'Académie des sciences en 2005. Après des travaux en géométrie analytique complexe, il s’est intéressé aux systèmes dynamiques, continus ou discrets, dans le champ complexe, à leurs relations, via les problèmes de divergence, avec les théories de Galois et à diverses applications, en particulier à des problèmes d’intégrabilité.
Pour en savoir plus : Bibliographie

