Qu'est-ce qu'une dimension fractale ?
On a inventé la notion de dimension pour classifier les ensembles négligeables de la droite. Selon É. Borel (1913), un ensemble de mesure nulle peut être inclus dans la réunion d'une infinité dénombrable d'intervalles $u_n$ tels que la série $\sum u_n$ converge, et tout point de $E$ appartient à une infinité de ces intervalles (nommés tout d'abord des intervalles d'exclusion). " Pour ces diverses raisons la notion d'ensemble de mesure nulle est primordiale; mais c'est en même temps une notion si générale qu'on ne peut espérer approfondir réellement cette notion qu'en étudiant de près cette notion générale, c'est-à-dire en ne confondant pas entre eux tous les ensembles de mesure nulle. La classification basée sur la décroissance asymptotique des intervalles d'exclusion me paraît être un premier pas dans cette étude qui s'impose aux analystes " [2]. En effet, la dimension sera toujours associée aux ordres de croissance des fonctions vers 0 ou vers l'infini.
1- Les indices associés à l'ensemble complémentaire
Borel y reviendra en 1948, à l'occasion d'un problème sur les fractions continues : à quelles conditions la somme de deux ensembles compacts de la droite est-elle de mesure nulle, ou bien au contraire contient-elle un intervalle ? Pour donner des conditions suffisantes, Borel définit divers indices de "raréfaction". Le compact $E$ est, dans un intervalle ouvert donné, le complémentaire d'une réunion au plus dénombrable d'intervalles ouverts $u_n$. Si $E$ est infini, et ne contient aucun intervalle, la suite $(u_n)$ est infinie. Supposons les $u_n$ rangés de fa\c{c}on que les longueurs $|u_n|$ forment une suite décroissante. La "raréfaction logarithmique" est
\[\rho=\limsup \frac{\log n}{\log n-\log\sum_{i=n}^{+\infty} |u_i|}.\]
Plus tard, mais sans doute indépendamment, Besicovitch et Taylor utiliseront pour majorer la dimension de Hausdorff un indice presque identique:
\[\liminf \frac{\log n}{\log n-\log\sum_{i=n}^{+\infty} |u_i|}.\]
Il existe bien d'autres indices du même type [11]. Le plus simple est sans doute
\[\limsup\frac{\ln n}{-\ln |u_n|},\]
qui peut aussi s'écrire comme l'indice de Taylor-Besicovitch
\[\inf\{\alpha : \sum_n|u_n|^\alpha<+\infty\}.\]
Ils seront généralisés au plan dans des études sur certaines surfaces poreuses.
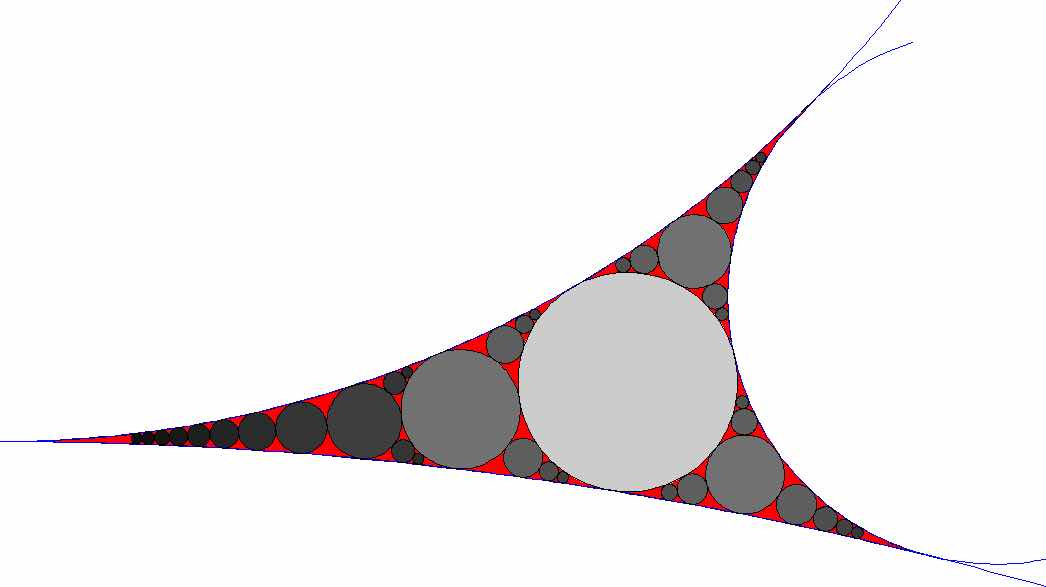
Par exemple, on a considéré l'ensemble résiduel de l'empilement apollonien, formé de cercles inscrits dans des triangles curvilignes. L'indice de Taylor-Besicovitch de la suite des diamètres peut être comparé à la dimension de Hausdorff (voir [12] pour des références générales).
2- Et ceux associés aux recouvrements
Mais auparavant, Bouligand avait introduit des indices fondés sur les recouvrements de $E$ par des intervalles [4]. Si $\omega_n$ désigne le nombre minimum d'intervalles de longueur $l^n$ recouvrant $E$ (en général on les prend dans un réseau), l'ordre dimensionnel de Bouligand est la limite, lorsqu'elle existe, du rapport
\[\frac{\ln \omega_n}{n\ln l}.\]
On peut aussi compter le nombre minimum $N_\epsilon (E)$ de boules de rayon $\epsilon$ recouvrant $E$, ou le nombre maximum $M_\epsilon (E)$ de boules disjointes de rayon $\epsilon$ centrées sur $E$, et considérer les rapports
\[\frac{\ln N_\epsilon (E)}{-\ln\epsilon}\quad,\quad\frac{\ln M_\epsilon (E)}{-\ln\epsilon}.\]
Ces trois rapports ont le même ordre de grandeur lorsque $n$ tend vers l'infini et $\epsilon$ vers 0.
En cas de convergence la limite est la célèbre dimension de boîtes.
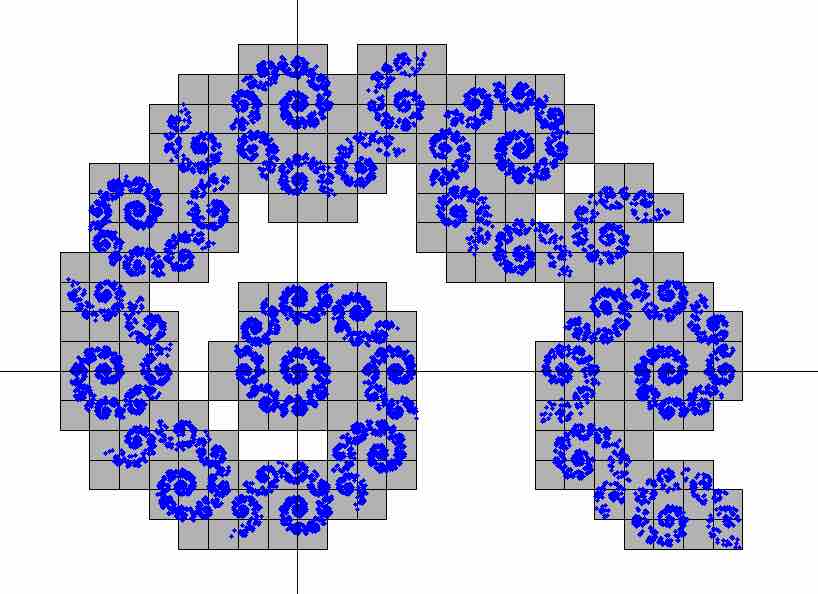
L'avantage de ces indices de recouvrement, c'est qu'ils sont faciles à généraliser en dimension 2 ou 3. L'indice
\[\liminf \frac{\ln N_\epsilon (E)}{-\ln\epsilon}\]
a été utilisé par Pontrjagin et Schnirelmann ordre métrique, pour comparaison avec la dimension topologique; et la limite supérieure par Hawkes dimension d'entropie. L'indice
\[\limsup \frac{\ln M_\epsilon (E)}{-\ln\epsilon}\]
est la dimension métrique de Kolmogorov. Il y a eu d'autres utilisations de ces indices, sous des vocables différents. Avons-nous donc affaire à une multitude de dimensions? Non, car tous ces indices de recouvrement coïncident entre eux [11]; et ils sont égaux à ceux associés aux intervalles complémentaires sur la droite, à condition que $E$ soit de mesure nulle. Les références sont nombreuses, mais la notion mathématique est toujours la même...[12].
Un avantage de la dimension de boîtes, c'est qu'on peut en donner une approximation numérique à partir de données réelles, à condition de bien définir les échelles du calcul et de donner un sens à la notion de limite. Mais pour les théoriciens, elle a l'inconvénient de ne pas tenir compte des propriétés topologiques de l'ensemble. En particulier, la dimension d'un ensemble borné est égale à celle de son adhérence! Bouligand avait lui-même remarqué que la dimension de l'ensemble $\{1,\frac 12, \dots, \frac 1n,\dots\}$ est $\frac 12$. Vue comme une limite supérieure, la dimension de boîtes, notée $\Delta$, a la propriété de stabilité [13] : $\Delta(E_1\cup E_2)=\max\{\Delta(E_1), \Delta(E_2)\}$, mais non celle de $\sigma$-stabilité : elle n'est pas stable pour une réunion dénombrable.
3- La dimension de Hausdorff
C'est Hausdorff [6] en 1919 qui, s'inspirant de la théorie de la mesure de Caratheodory, précise le mieux à son époque la notion de dimension, du point de vue de la théorie de la mesure. On se donne un réel $\alpha>0$. Pour tout $\epsilon>0$, on considère tous les recouvrements possibles de $E$ par des ensembles de diamètre $\le\epsilon$ :
\[H_\epsilon^\alpha(E)=\inf\{\sum_n \mbox{diam}(E_n)^\alpha : E\subset\cup E_n, \mbox{diam}(E_n)\le\epsilon\}.\]
Cette quantité est une fonction décroissante de $\epsilon$. Elle a donc une limite (éventuellement $+\infty$) lorsque $\epsilon$ tend vers 0. La mesure de $E$ en dimension $\alpha$ est $H^\alpha(E)=\lim_{\epsilon\to 0}H_\epsilon^\alpha(E)$. Il s'agit d'une mesure extérieure au sens de Caratheodory. On observe qu'elle prend les valeurs 0 ou $+\infty$, sauf éventuellement pour une valeur de coupure qui est la dimension de Hausdorff :
\[\dim_H(E)=\inf\{\alpha : H^\alpha(E)=0\}=\sup\{\alpha : H^\alpha(E)=+\infty\}.\]
Les mesures de Hausdorff forment toute une famille de mesures intermédiaires entre les mesures de longueur, d'aire, de volume, etc. Il suffit de changer la valeur de $\alpha$. De même, $\dim_H(E)$ est une dimension fractionnaire, qui fait l'interpolation entre la dimension 1 du segment, 2 du disque, 3 de la sphère...
Ce sera le point de départ de nombreux travaux de Besicovitch. On peut remarquer le commentaire, un peu critique, de Borel [3] à ce sujet : "Je dois tout d'abord faire observer que la méthode de M. Besicovitch présente avec la mienne une différence analogue entre ma définition de mesure des ensembles et la définition de M. Lebesgue". En effet Borel était un adepte des mathématiques constructives. La dimension de Hausdorff, définie à partir de bornes inférieures, ne se construit pas numériquement. Il faudra donc distinguer entre deux types de dimensions : les dimensions théoriques, appréciées du mathématicien, et dont la valeur ne se calcule que sur des ensembles d'un type particulier; et les dimensions de portée plus pratique, dont on peut donner des estimations sur les données numériques, mais qui s'insèrent mal dans un traité de Théorie Géométrique de la Mesure. Les unes sont $\sigma$-stables, car elles proviennent d'une famille de mesures; et les autres non.
Dans [13] on trouvera une autre définition de dimension, qui provient également d'une famille de mesures : la dimension d'empilement ou packing dimension. Au lieu de recouvrir l'ensemble $E$, on préfère considérer des boules disjointes centrées sur $E$ (empilements} pour définir une autre famille de mesures. La dimension correspondante se comporte comme la symétrique de la dimension de Hausdorff dans de nombreux résultats (les $\liminf$ sont remplacées par des $\limsup$ etc.).
À l'époque où la mode des fractales, due à B. Mandelbrot, a décollé, il y a eu beaucoup de confusion sur ces notions de dimension. De nombreux chercheurs ont admis allègrement que la dimension de boîtes était une bonne approximation de la dimension de Hausdorff. L'inégalité $\dim_H(E)\le\Delta(E)$ est toujours vraie, mais l'égalité ne se produit que sur des ensembles bien particuliers; le type le plus connu est celui des ensembles à similitude interne, ou auto-similaire pour employer une mauvaise traduction du self-similar anglais. Ainsi la courbe de Von Koch est la réunion de 4 images d'elle-même par des similitudes de rapport $\frac 13$, et sa dimension (de boîtes, de Hausdorff, ...) vaut $\frac{\ln 4}{\ln 3}$. Mais dès qu'on étudie les ensembles auto-affines, les dimensions peuvent être différentes. Par exemple, pour la courbe de McMullen on trouve [8] $\Delta(E)=\frac 32$ et $\dim_H(E)=\ln(1+\sqrt{3})/\ln 2$.
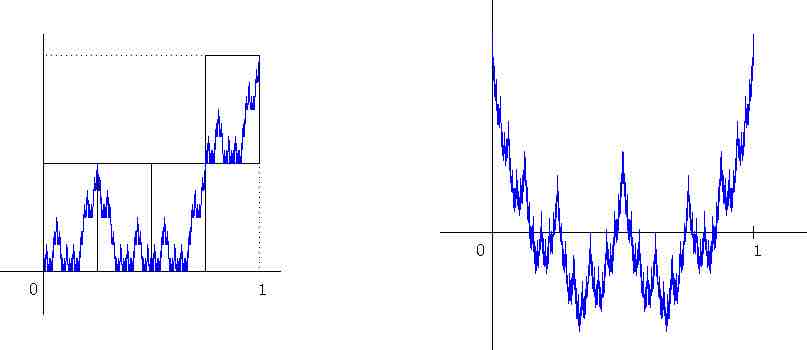
Pour la courbe de la fonction de Weierstrass, définie pour tout $x$ comme
\[W_H(x)=\sum_{n=0}^{+\infty} \omega^{nH}\cos(\omega^n x+\phi_n)\]
où $\omega>1$, $0<H<1$, et $(\phi_n)$ est une suite quelconque de phases, on peut vérifier que $\Delta(E)=2-H$.
4- L'ensemble de Mandelbrot
La dimension de Hausdorff de la frontière de l'ensemble de Mandelbrot vaut 2. Ce résultat, conjecturé par Mandelbrot, a été démontré en 1990 par M. Shishikura [10]. Il reste une conjecture : cette frontière est d'aire (mesure de Lebesgue) nulle. On sait aussi que pour un ensemble dense de nombres complexes $c$ dans cette frontière, l'ensemble de Julia $J_c$ est de dimension 2. Il existe même des ensembles de Julia d'aire non nulle [5].

5- Le mouvement brownien
La trajectoire du mouvement brownien dans le plan est une courbe fractale bien connue. On sait depuis longtemps que presque sûrement la dimension de la trajectoire est 2, ce qui est le maximum dans le plan. B. Mandelbrot avait conjecturé que la dimension de la frontière extérieure (ou de celle des petites îles entourées par la trajectoire) était égale à $\frac 43$. Cette conjecture a été démontrée récemment (voir [1] pour une présentation générale).

[1] V. Beffara. « Raconte-moi le processus SLE ». Gazette des mathématiciens 144 (2015), p. 59–63.
[2] É. Borel. « Les ensembles de mesure nulle ». Bull. Soc. Math. Fr. 41 (1913), p. 1–19.
[3] É. Borel. « Sur les ensembles de mesure nulle ». Physical Review 25 (1935), p. 7–19.
[4] G. Bouligand. « Ensembles impropres et nombre dimensionnel ». Bull. Sc. math. 52 (1928), p. 320–376.
[5] X. Buff et A. Chéritat. « Quadratic Julia sets with positive area ». Ann. of Math. 176 (2012), p. 673–746.
[6] F. Hausdorff. « Dimension und äusseres Mass ». Math. Ann. 79 (1919), p. 157–179.
[7] B. Hunt. « The Hausdorff dimension of graphs of Weierstrass functions ». Proc. Amer. Math. Soc. 126 (1998), p. 791–800.
[8] C. McMullen. « The Hausdorff dimension of general Sierpinski carpets ». Nagoya Math. J. 96 (1984), p. 1–9.
[9] W. Shen. « Hausdorff dimension of the graphs of the classical Weierstrass functions ». arXiv:1505.03986v1 [math.DS] (mai 2015).
[10] M. Shishikura. « The Hausdorff dimension of the boundary of the Mandelbrot set and Julia sets ». Ann. of Math. 147 (1998), p. 225–267.
[11] C. Tricot. « Douze définitions de la densité logarithmique ». Physical Review 293 (1981), p. 549–552.
Claude Tricot est professeur à l’université Blaise Pascal de Clermont-Ferrand, après un début de carrière en Angleterre et au Canada. Il a participé à l’émergence de la géométrie fractale dans les années 80, en particulier en introduisant les mesures et la dimension de packing.

