Raconte-moi... KAM
par Marie-Claude Arnaud
I- Les systèmes hamiltoniens
Les systèmes hamiltoniens modélisent de très nombreux systèmes physiques, qu'on appelle aussi parfois conservatifs, pour lesquels une quantité particulière, l'énergie, est conservée.
On peut les définir sur n'importe quelle variété, mais pour simplifier nous allons les introduire sur $\mathbb{R}^n\times \mathbb{R}^n$, ou sur $\mathbb{T}^n\times \mathbb{R}^n$ où $\mathbb{T}=\mathbb{R}/\mathbb{Z}$. On se donne une fonction $H:\mathbb{R}^n\times \mathbb{R}^n\rightarrow \mathbb{R}$ de classe $C^2$, qu'on appelle {\sl hamiltonien}. Les équations de Hamilton associées sont des équations différentielles dont on note $t\mapsto (q(t), p(t))\in \mathbb{R}^n\times\mathbb{R}^n$ les solutions:
\[
\frac{dq}{dt}=\frac{\partial H}{\partial p}(q, p)\quad{\rm et}\quad \frac{dp}{dt}=-\frac{\partial H}{\partial q}(q, p).
\]
Ainsi, à un système issu de la mécanique classique décrit par un potentiel $V:\mathbb{R}^n\rightarrow \mathbb{R}$
\begin{equation}\label{eqclass2}m\frac{d^2q}{dt^2}=\frac{\partial V}{\partial q} \quad (1)\end{equation}
où $q$ représente la position d'un point massif de masse $m$, on associe le hamiltonien $H:\mathbb{R}^n\times \mathbb{R}^n\rightarrow \mathbb{R}$ défini par
\[
H(q, p)=\frac{1}{2m}\| p\|^2-V(q).
\]
Les équations de Hamilton sont
\begin{equation}\label{eqclass}\frac{dq}{dt}=\frac{p}{m}\quad{\rm et}\quad \frac{dp}{dt}=\frac{\partial V}{\partial q}(q). \quad (2)\end{equation}
Alors, $(q, p)$ est solution de (2) si et seulement si $q$ est solution de (1) et $p=m\frac{dq}{dt}$ est la quantité de mouvement.
Remarquez que le hamiltonien s'écrit en fonction de $q$ et $\frac{dq}{dt}$ comme
\[
H=\frac{m}{2}\left\| \frac{dq}{dt}\right\|^2-V(q)
\]
c'est-à-dire comme l'énergie totale du système, somme de l'énergie cinétique et de l'énergie potentielle.
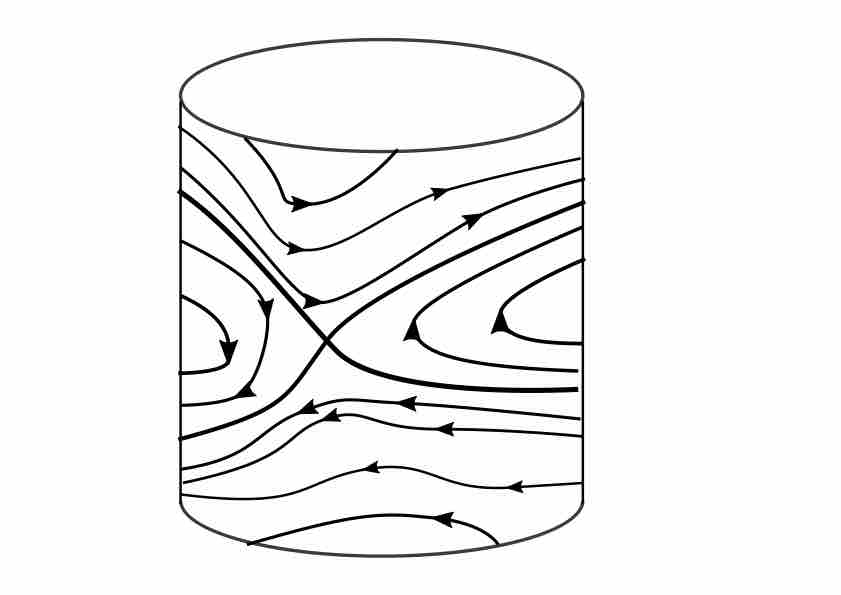
C'est une propriété générale que le hamiltonien est constant le long des orbites hamiltoniennes (on dit que le hamiltonien est une intégrale). Ses orbites restent donc dans les niveaux d'énergie $\{ H={\rm constante}\}$.
II- Le problème de la stabilité et les systèmes intégrables
Il y a un système très classique qui est décrit par un potentiel. Il s'agit du problème des $N$-corps : $N$ corps massifs soumis à la force d'attraction universelle. Le potentiel pour $N$-corps en positions $q_1, \dots, q_N$ de masses $m_1, \dots, m_N$ est
\[
V(q)=\sum_{1\leq i<j\leq N} \frac{m_im_j}{\| q_i-q_j\|}.
\]
On connaît depuis Newton les équations différentielles qui gouvernent les mouvements des planètes, mais dès qu'il y a au moins trois corps, on ne sait pas calculer explicitement les solutions. On aimerait pourtant répondre à une question qui est extrêmement naturelle : notre système solaire va-t-il continuer d'exister plus ou moins comme actuellement ou va-t-il connaître des changements dramatiques, comme une planète qui partirait à l'infini ou comme deux planètes qui entreraient en collision?
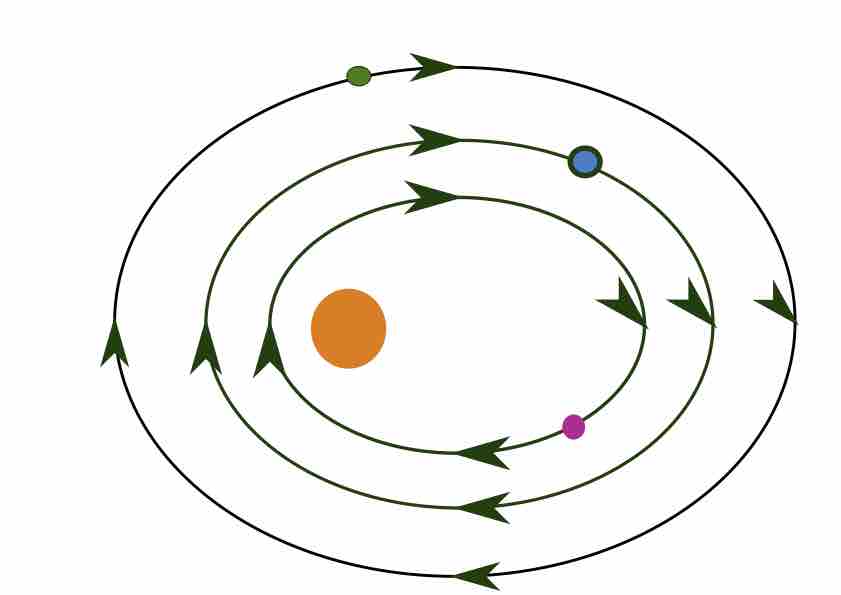
Ce système hamiltonien est en fait compliqué, et avant d'y revenir, décrivons les systèmes hamiltoniens les plus simples qui soient, ceux qu'on appelle complètement intégrables.
L'exemple "bébé" est donné par une fonction $H: \mathbb{T}^n\times \mathbb{R}^n\rightarrow \mathbb{R}$ qui ne dépend que de la deuxième coordonnée $p\in \mathbb{R}^n$:
$H(q,p )= h(p)$. Les équations de Hamilton sont alors
\[
\frac{dq}{dt}=\frac{d h}{d p}(p)\quad{\rm et}\quad \frac{dp}{dt}=0.
\]
L'évolution du système dynamique associé aux équations de Hamilton est décrite par son flot $(\varphi_t^H)_{t\in\mathbb{R}}$1. Le flot au temps $t$, $\varphi^H_t: \mathbb{T}^n\times\mathbb{R}^n\rightarrow \mathbb{T}^n\times \mathbb{R}^n$ est un difféomorphisme défini comme suit : à tout $x_0=(q_0,p_0)\in \mathbb{T}^n\times \mathbb{R}^n$, si $x:\mathbb{R}\rightarrow\mathbb{T}^n\times \mathbb{R}^n$ désigne la solution telle que $x(0)=x_0$, alors $\varphi^H_t(x_0)=x(t)$.
Dans notre exemple précis, le flot est donné par
\[
\varphi_t^H(q, p)=(q+t\frac{d h}{d p}(p), p).
\]
On observe que $\mathbb{T}^n\times \mathbb{R}^n$ est feuilleté par les tores $\mathbb{T}^n\times\{ p_0\}$ qui sont tous invariants par le flot hamiltonien, et que la restriction du flot à chacun de ces tores est le flot de rotation $(q, p_0)\mapsto (q+t\alpha, p_0)$ engendré par $\alpha=\frac{d h}{d p}(p_0)$.
En particulier, toutes les orbites sont bornées et on peut dire qu'un tel système est stable.
Plus généralement, un hamiltonien $H$ est dit complètement intégrable sur un ouvert $U\subset \mathbb{T}^n\times \mathbb{R}^n$ invariant par le flot s'il existe $n$ fonctions de classe $C^2$ $H_1, \dots, H_n: U\rightarrow \mathbb{R}$ telles que
- les fonctions $H_i$ sont toutes constantes le long des orbites contenues dans $U$ (on parle alors d'intégrales premières) ;
- les flots hamiltoniens des $H_i$ commutent deux à deux ;
- en chaque $x\in U$, les formes linéaires $dH_1(x)$, \dots, $dH_n(x)$ sont linéairement indépendantes.
Le théorème d'Arnold-Liouville (voir [1]) dit que sous ces hypothèses, si une composante connexe $\mathcal{N}$ d'un $n$-niveau $\{ H_1=c_1, \dots , H_n=c_n\}$ est compacte, alors il existe un voisinage $\mathcal{V}$ de $\mathcal{N}$ dans $U$, un voisinage $V$ de $0$ dans $\mathbb{R}^n$ et un difféomorphisme $\psi: \mathcal{V}\rightarrow \mathbb{T}^n\times V$ tels que
- $\psi (\mathcal{V})=\mathbb{T}^n\times V$;
- il existe un hamiltonien $K:\mathbb{T}^n\times V\rightarrow \mathbb{R}$ qui ne dépend que de $p\in V$ tel que sur $\mathcal{V}$, on a
\[
\varphi_t^H=\psi^{-1}\circ \varphi_t^K\circ \psi.
\]
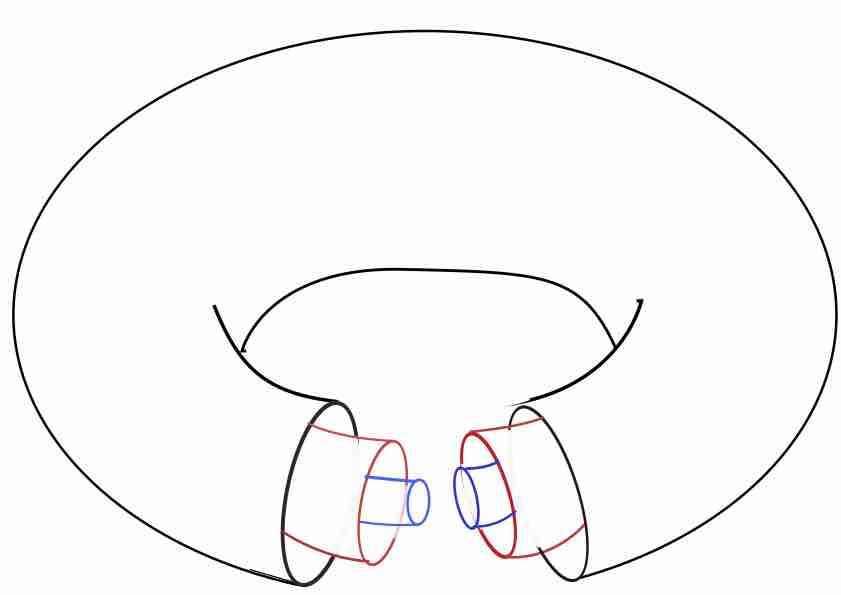
En d'autres termes, quitte à faire un changement de coordonnées sur un voisinage tubulaire $\mathcal{V}$ du tore $\mathcal{N}$, on s'est ramené à l'exemple bébé : $\mathcal{V}$ est feuilleté par des tores plongés invariants sur lesquels la dynamique est conjuguée à un flot de rotations. En particulier, une condition initiale près de $\mathcal{N}$ donne une orbite entière près de $\mathcal{N}$: on a stabilité.
Il existe des exemples classiques de systèmes complètement intégrables, comme le flot géodésique sur un ellipsoïde.
Mais a priori le système solaire et le problème des $N$-corps ne sont pas complètement intégrables2.
III- Retour sur le problème des $N$-corps: séries de Lindstedt et problème des petits dénominateurs
Dans son ouvrage maintenant classique Les méthodes nouvelles de la mécanique céleste}, Henri Poincaré s'intéresse au problème des $N$-corps3.
On commence par partir d'un système imaginaire où on ne considère que les interactions Soleil-Planète mais pas les interactions mutuelles entre les planètes. On a ainsi huit problèmes de Kepler (problèmes à deux corps où le mouvement s'effectue suivant des ellipses, chaque problème correspondant au soleil et une planète) indépendants, qu'on peut aussi voir comme huit oscillateurs indépendants. Mathématiquement, même si cela peut sembler étrange au lecteur, cela revient à supposer que les planètes sont toutes de masse nulle. Ce système est complètement intégrable mais peu conforme à la réalité.
L'idée de Linstedt est alors de perturber le système en supposant les masses des planètes "petites" (c'est-à-dire toutes proportionnelles à un même petit paramètre $\mu$). On cherche alors des tores invariants qui soient des perturbations des tores invariants qui apparaissaient dans le cas complètement intégrable (quand $\mu=0$), dont l'équation s'écrit comme une série entière en $\mu$. Pour trouver chaque coefficient de ce développement en puissances de $\mu$, on utilise l'équation de Hamilton (ou plutôt celle qui s'appelle l'équation de Hamilton-Jacobi mais qui n'est pas l'objet de ce texte) et on obtient chacun de ces coefficients comme une série formelle en fonctions trigonométriques des coordonnées $y=(y_1, \dots, y_n)$ comme suit
\[
\alpha_{1}y_1+\alpha_{2}y_2+\dots +\alpha_{n}y_n
\]
\[
+\sum\frac{B\sin (k_1y_1+k_2y_2+\dots +k_ny_n)}{k_1.f_1+k_2.f_2+\dots +k_n.f_n}
\]
\[
+\sum\frac{C\cos (k_1y_1+k_2y_2+\dots +k_ny_n)}{k_1.f_1+k_2.f_2+\dots +k_n.f_n}
\]
où les $k_i$ parcourent l'ensemble des entiers non tous nuls et les $f_i$ sont les fréquences des mouvements découplés : en d'autres termes, sur le tore considéré avant perturbation, le mouvement était conjugué à $t\mapsto (\theta_1+tf_1, \dots, \theta_n+tf_n)$.
On constate de suite un problème pour les $(f_1, \dots, f_n)$ qui forment une famille liée sur $\mathbb{Q}$, car alors un des dénominateurs s'annule et la méthode ne s'applique pas: on parle alors de résonance. Même dans le cas où la famille des fréquences est libre sur $\mathbb{Q}$, certains dénominateurs sont très proches de $0$ : on parle alors de petits dénominateurs. On ne peut donc jamais assurer la convergence de la série... sauf si on sait contrôler les coefficients $B$ et $C$.
Poincaré ne savait pas contrôler ces coefficients, et il a fallu attendre une cinquantaine d'années avant d'avoir une réponse positive (mais dépendant des fréquences considérées) sur la convergence.
Comme le dit François Béguin dans l'excellent texte [3]) : Poincaré a montré qu'il y a un risque que le système solaire soit instable, et Kolmogorov, Arnol'd et Moser ont montré qu'il y a de bonnes chances pour qu'il soit stable.
IV- La genèse des théorèmes K.A.M.
En 1954, Andreï Kolmogorov annonça que sous certaines hypothèses de non-dégénérescence, beaucoup de tores invariants d'un système analytique complètement intégrable persistent sous une perturbation analytique assez petite. L'article ne comportait pas de preuve complète des résultats.
Le jeune Jürgen Moser fut sollicité comme rapporteur par les Math Reviews. Il développa une machinerie puissante qui donna la première démonstration du résultat de Kolmogorov, mais dans un cas suffisamment différentiable au lieu d'analytique. Moser publia ses résultats en 1962. Un an après, Vladimir Arnol'd, un brillant élève de Kolmogorov, publia sa preuve du théorème de Kolmogorov dans le cadre original ;
la preuve d'Arnol'd s'applique au problème des $N$-corps ; c'est pourquoi ces résultats sont maintenant connus sous l'acronyme K.A.M (les articles fondateurs étant [8], [10]) et [2]).
Les tores qui persistent sont ceux dont les fréquences sont diophantiennes, où un nombre $f= (f_1, \dots , f_n)$ est dit diophantien s'il existe $\gamma>0$ et $\tau>0$ tels que pour tout $p=(p_1, \dots, p_n)\in \mathbb{Z}^n$, tout $q\in\mathbb{Z}$ tels que $(p,q )\not= {\bf 0}_{\mathbb{R}^{n+1}}$, on a
\[
| f.p-q|\geq \frac{\gamma}{\left( q^2+\sum_{k=1}^n p_k^2 \right)^\frac{\tau}{2}}.
\]
Un tel $f$ est dit $(\gamma, \tau)$-diophantien. L'ensemble des nombres diophantiens est alors un ensemble maigre au sens de Baire mais de mesure de Lebesgue pleine.
Le théorème K.A.M. dans le cas $C^\infty$ s'énonce comme suit.
Soit $V$ un voisinage de $0$ dans $\mathbb{R}^n$ et $H_0:\mathbb{T}^n\times V\rightarrow \mathbb{R}$ un hamiltonien de classe $C^\infty$ complètement intégrable: $H(q, p)=h(p)$. On note $\mathcal{F}(p)=(\frac{\partial h}{\partial p_1}(p), \dots, \frac{\partial h}{\partial p_n}(p))$ le vecteur des fréquences. Soit $p_0\in V$. On suppose
- $\mathcal{F}(p_0)$ est $(\gamma, \tau)$-diophantien ;
- hypothèse de non dégénérescence : $D\mathcal{F}(p_0)$ est inversible.
Alors il existe un voisinage $\mathcal{U}$ de $H_0$ dans $C^\infty(\mathbb{T}^n\times V, \mathbb{R})$ tel que tout $H$ dans $\mathcal{U}$ a un tore invariant $\mathcal{T}_H$ par le flot $(\varphi_t^H)$ qui est
- le graphe d'une application $u_H:\mathbb{T}^n\rightarrow V$;
- tel que $(\varphi_t^H)$ restreint à $\mathcal{T}_H$ est conjugué au flot de rotation engendré par $\mathcal{F}(p_0)$.
De plus $u_H$ dépend continûment de $H$.
Donnons quelques compléments
- la conjugaison sur le tore dépend aussi contin\^ument de $H$ ;
- à condition de supposer $H$ de classe $C^k$ avec $k>2\tau +2$, on a aussi un résultat en régularité finie (alors $u_H$ est de classe $C^{k-2\tau}$) ;
- il est possible d'utiliser le théorème simultanément pour différentes valeurs de $p_0$. À $\gamma$ et $\tau$ fixés, on trouve pour $H$ assez proche de $H_0$ toute une famille de tores invariants, de fréquences $(\gamma, \tau)$-diophantiennes et dont la réunion est de mesure de Lebesgue non nulle ;
- en fait les tores K.A.M. n'arrivent jamais seuls: ils sont toujours accumulés par d'autres tores K.A.M.
Un nouveau concept de stabilité est né, qui ne s'applique pas pour toutes les orbites mais pour une majorité d'entre elles. En général, on observe des régions de stabilité remplies de tores K.A.M, et d'autres dites chaotique (mais c'est une autre histoire).
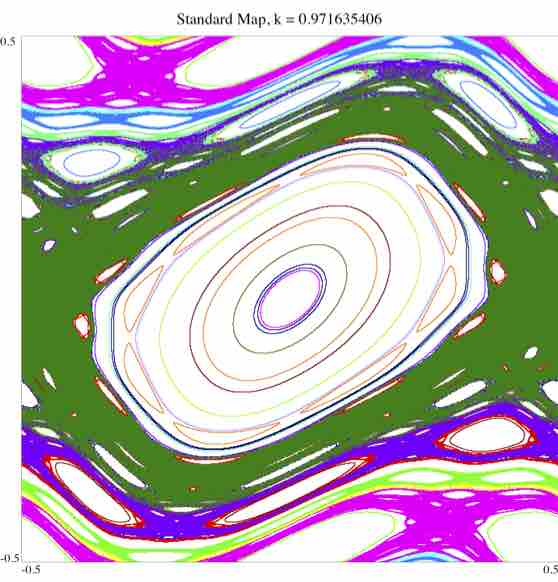
V- Prolongements
1- Quelques applications des théorèmes K.A.M
Pour le problème des $N$-corps, le hamiltonien ne vérifie pas l'hypothèse de non-dégérescence et c'est pourquoi Arnol'd donna une version du théorème qui s'applique à des cas dégénérés comme le problème des $N$-corps. Toutefois, cette démonstration n'était complète que pour 3 corps dans le plan et c'est M. Herman qui donna une démonstration complète de ce qui se passe pour $N$-corps (voir [7]).
En résumé, les séries qui apparaissent dans le problème des $N$-corps sont convergentes pour certains choix des fréquences et divergentes pour d'autres.
Dans l'article [11], Jürgen Moser explique aussi pourquoi la théorie K.A.M. permet d'apporter une justification théorique au fonctionnement des accélérateurs de particules.
Dans l'article [10], Jürgen Moser parle en fait de difféomorphismes symplectiques plutôt que de systèmes hamiltoniens, car il existe des énoncés dans les deux contextes et une façon standard de passer d'un des deux cadres à l'autre (voir aussi [4]). L'application des théorèmes K.A.M. dans le contexte des applications plutôt que des hamiltoniens permet par exemple de montrer
- la stabilité au voisinage des points fixes des difféomorphismes génériques des surfaces qui préservent l'aire;
- la stabilité au voisinage des bords des billards dits de Birkhoff (billards plans à bord régulier et strictement convexe).
2- D'autres résultats K.A.M
En fait, les théorèmes K.A.M. donnent des résultats pour des systèmes dynamiques qui ne sont pas forcément complètement intégrables (voir par exemple [5]).
L'idée est la suivante. On suppose que le système hamiltonien a un tore invariant sur lequel la dynamique est conjuguée à un flot de rotation diophantien. Alors, en quelque sorte, on linéarise la dynamique au voisinage de ce tore (on utilise une forme normale). Si une certaine condition de non dégénérescence est satisfaite le long du tore, alors
- si on fait une perturbation petite en topologie $C^\infty$ du hamiltonien, le nouvel hamiltonien a aussi un tore invariant portant la même dynamique;
- sans perturber, le tore invariant est lui-même accumulé par une infinité de tores invariants sur lesquels la dynamique est conjuguée à un flot de rotation diophantien.
VI- Références
[1] V. ARNoL’D. Les méthodes mathématiques de la mécanique classique. Traduit du russe par Djilali Embarek. Éditions Mir, Moscow, 1976, p. 470.
[2] V. I. ARNoL’D. « Proof of a theorem of A. N. Kolmogorov on the preservation of conditionally periodic motions under a small perturbation of the Hamiltonian». Uspehi Mat. Nauk 18, no 5 (113) (1963), p. 13–40.
[3] F. BÉGuiN. « Le mémoire de Poincaré pour le prix du roi Oscar: l’harmonie céleste empêtrée dans les intersections homoclines ». L’héritage scientifique de Poincaré. Belin, Paris (2006), p. 177–209.
[4] J.-B. BosT. « Tores invariants des systèmes dynamiques hamiltoniens (d’après Kolmogorov, Arnol’d, Moser, Rüssmann, Zehnder, Herman, Pöschel,...) » Astérisque, no 133-134 (1986). Seminar Bourbaki, Vol. 1984/85, p. 113–157.
[5] L. H. ELiAssoN, B. FAyAD et R. KRikoRiAN. « Around the stability of KAM tori ». Duke Math. J. 164, no 9 (2015), p. 1733–1775.
[7] J. FÉjoz. « Démonstration du ‘théorème d’Arnold’ sur la stabilité du système planétaire (d’après Herman) ». Ergodic Theory and Dynamical Systems 24, no 05 (2004), p. 1521–1582.
[6] J. FÉjoz. « Le problème de la stabilité du Système solaire, de Lagrange à nos jours». Deux cents ans après Lagrange (2013), p. 1–30. uRL : https://www.ceremade.dauphine.fr/~fejoz/articles.php.
[8] A. N. KoLMoGoRov. « On conservation of conditionally periodic motions fora small change in Hamilton’s function ». Dokl. Akad. Nauk SSSR (N.S.) 98 (1954), p. 527–530.
[9] J. MEiss. Std Map 4.5. uRL : https://amath.colorado.edu/faculty/jdm/stdmap.html.
[10] J. MosER. « On invariant curves of area-preserving mappings of an annulus ». Nachr. Akad. Wiss. Göttingen Math.-Phys. Kl. II 1962 (1962), p. 1–20.
[11] J. MosER. « Is the solar system stable? » Math. Intelligencer 1, no 2 (1978/79), p. 65–71.
Notes :
1. Pour simplifier, on supposera les solutions définies sur $\mathbb{R}$ tout entier.
2. On sait montrer dans certains cas qu'il n'existe pas assez d'intégrales qui soient analytiques réelles pour le problème des $N$-corps. Par contre, à ma connaissance, il n'existe pas de tels résultats concernant la non-intégrabilité $C^\infty$.
3. Sur l'aspect historique, voir aussi le texte [6] de Jacques Féjoz.

Marie-Claude Arnaud
Université d'Avignon.
Marie-Claude Arnaud est professeur de mathématiques. Elle travaille sur les systèmes dynamiques symplectiques et s’intéresse plus particulièrement aux ensembles invariants qui sont moins réguliers que la dynamique.
Originellement paru dans le n°149 (juillet 2016) de la Gazette.

